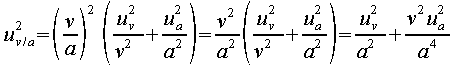Retour au sommaire du dossier |  Retour à l'accueil

Incertitude-type sur un facteur de dilution (dilution unique ou dilutions en série)

1. Facteur de dilution de type a/(a+b)

Soit d une dilution : d = a/(a+b)
a étant le volume de prise d'essai et b le volume de diluant auquel on a rajouté a.

Soit f le facteur de dilution inverse f = (a+b)/a

On montre que :	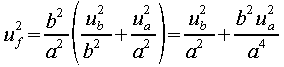Ui est le symbole de l'incertitude-type de la variable i (écart-type) ; (donc u est une variance) u2f , u2a , u2b représentent respectivement les variances sur f, a et b.
Démonstration. En effet : f = (a+b)/a = 1 + b/a donc u2f = u2b/a or puisque a et b sont des variables indépendantes (lien vers un rappel de maths)

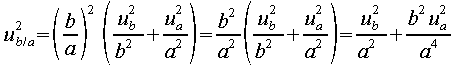2. Facteur de dilution de type a/v

Soit d une dilution : d = a/v
a étant le volume de prise d'essai et v le volume final auquel la solution a été amenée par du diluant grâce à l'utilisation d'un récipient jaugé de type "in".

Soit f le facteur de dilution inverse f = v/a

On montre que : Puisque v et a sont des variables indépendantes (lien vers un rappel de maths)

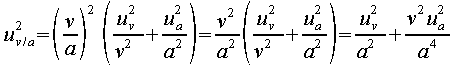Ui est le symbole de l'incertitude-type de la variable i (écart-type) ; (donc u est une variance) u2f , u2a , u2b représentent respectivement les variances sur f, a et v.

3. Dilutions en série

Soit k étapes de dilutions en série : d₁, d₂ ... d_k. Soit les facteurs inverses correspondant : f₁, f₂ ... f_k. Soit F le facteur inverse global de dilution : F = Πf_i.

On a donc u_F² = F² ( u_f1² / f₁² + u_f2² / f₂² + ... + u_fk² / f_k²) = F² [Σ (u_fi / f_i )²]

On utilise la loi de propagation des écart-types appliquée à un produit de variables indépendantes : (lien vers un rappel de maths dans une nouvelle fenêtre)

Si on applique au cas particulier, très fréquent en biologie de laboratoire, de dilutions à l'identique en série. Soit f le facteur de dilution inverse da chaque dilution particulière. Soit k dilutions en série. Soit F le facteur global inverse de dilution F = f^k. On a :

u_F² = F²k (u_f² / f²)

On utilise la loi de propagation des écart-types appliquée à un produit de variables indépendantes : (lien vers un rappel de maths dans une nouvelle fenêtre)

4. Exemple

Soit 5 dilutions en série de type 1 mL (a) ajouté à 9 mL (b) de diluant. d=1/10 ; f=10.

Soit par exemple (cas typique en microbiologie, dénombrement d'Unités Formant Colonies avec un matériel standard) :
u_a = 0,01 mL et u_b = 0,2 mL.

On obtient :
u_f² = (0,2²/1²) + (9²*0,01²/1⁴) = 0,0481

Soit :
u_F² = 10⁵²*5*(0,0481/10²) = 240 10⁵

Soit :
u_F = 4904
Soit :
u_F / F = 4904 / 10⁵ = 0,049 # 5%

Retour au sommaire du dossier | Retour à l'accueil |   Droits de copie  |  A propos de l'auteur  | JF Perrin - 2005/2007 - jef.perrin.free.fr