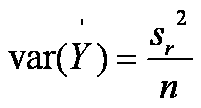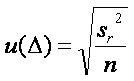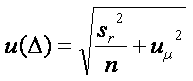Retour au
sommaire du dossier | Retour
à l'accueil
Biais de laboratoire d'un laboratoire Li et ISO
5725-4
On suppose une méthode de dosage pour laquelle la
fidélité (répétabilité et
reproductibilité) a établi à la suite d'une
étude interlaboratoire selon la norme ISO-5725.
On rappelle quelques définitions [ISO 3534-1]
:
Justesse. Étroitesse de l’accord entre la
valeur moyenne obtenue à partir d’une large
série de résultats d’essais et une valeur de
référence acceptée.
NOTES :
La mesure de la justesse est généralement
exprimée en termes de biais. La justesse a
été également appelée
« exactitude de la moyenne ». Cet usage n’est
pas recommandé.
Biais. Différence entre l'espérance
mathématique des résultats d'essai et une valeur de
référence acceptée.
NOTE :
Le biais est l'erreur systématique totale par opposition
à l’erreur aléatoire. Il peut y avoir une ou
plusieurs composantes d'erreur systématique qui
contribuent au biais. Une différence systématique
plus importante par rapport à la valeur de
référence acceptée est
reflétée par une plus grande valeur du biais.
Biais de la méthode de mesure. Différence
entre l'espérance mathématique des résultats
d'essais obtenus à partir de tous les laboratoires
utilisant cette méthode et une valeur de
référence acceptée.
Le biais de la méthode de mesure est mesuré par le
déplacement de la moyenne des résultats d'un grand
nombre de laboratoires différents utilisant tous la
même méthode. Le biais de la méthode de
mesure peut être différent pour différents
niveaux.
Biais du laboratoire. Différence entre
l'espérance mathématique des résultats
d'essai d'un laboratoire particulier et une valeur de
référence acceptée.
Composante laboratoire du biais. Différence
entre le biais du laboratoire et le biais de la méthode de
mesure.
NOTES :
La composante laboratoire du biais est spécifique à
un laboratoire donné et aux conditions de mesure dans ce
laboratoire et peut également être
différente à différents niveaux de
l’essai.. La composante laboratoire du biais est relative
au résultat de la moyenne générale et
non à la valeur vraie ou de référence.
On peut alors s'attaquer au problème de la
détermination du bais de laboratoire d'un laboratoire Li
selon ISO 5725 :
abréviations utilisées :
µ : valeur du MRC soumis à étude inter
laboratoires ; uµ : incertitude-type sur
µ ; Δ : biais du laboratoire Li le jour de
l'expérience ; Ý : la meilleure estimée du
laboratoire Li selon n mesurages en conditions de
répétabilité (donc sa moyenne le jour
donné de l'expérience, en conditions de
répétabilité) ; var signifie variance
; sr : écartype de
répétabilité établi au terme de
l'étude inter laboratoires ; sL :
écartype inter-laboratoires établi au terme de
l'étude inter laboratoires ; sR :
écartype de reproductibilité établi au terme
de l'étude inter laboratoires ; on rappelle
(sR)2 = (sL)2 +
(sr)2.
|
Δ = Ý - μ
var(Δ) = var(Ý) +
var(μ)
avec
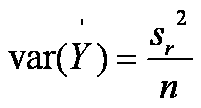
Il faudra vérifier que la
répétabilité du laboratoire Li est bien
assimilable à la répétabilité de la
méthode au niveau choisi (soit dans le cadre de
l'étude inter laboratoires dans laquelle pourrait se
situer la détermination du biais de laboratoire du
laboratoire Li, soit par un test de Khi² permettant de
comparer la répétabilité de la
méthode au niveau choisi -et établie selon
expérience inter laboratoires- et l'écart-type de
répétabilité obtenu par le laboratoire Li
testé au momment de la détermination de son biais
de laboratoire du jour).
|
|
La norme ISO 5725-4 suppose que
uµ négligeable d'où :
|
Un calcul plus général serait, je
crois :
|
|
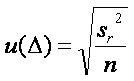
|
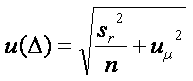
|
|
Et l'intervalle de confiance sur Δ est
[Δ - 1,96 uΔ ; Δ + 1,96
uΔ]
Si la valeur zéro (0) est dans l'intervalle de
confiance de Δ, on pourra dire qu'on n'a pas montré
l'existence d'un biais de laboratoire du laboratoire Li au risque
0,05 (risque alpha), le jour de l'expérience.
Remarque : Le modèle pour un mesurage y
le jour de l'expérience est y=µ+δ+B+e avec
μ valeur vraie, δ biais de la méthode, B
composante laboratoire du biais et e aléa du à la
répétabilité.
Et on a Δ = δ+B
Or B est a priori changeant au jour le jour si il y a par exemple
un étalonnage chaque jour ...donc l'expérience de
détermination de biais de laboratoire est à
inscrire dans ce cadre et dans ce cadre seulement : elle est
réalisée sur une série de mesurages en
conditions de répétabilité !
|
Retour au
sommaire du dossier | Retour
à l'accueil |
Droits de copie.
|
A propos de l'auteur
| JF Perrin - 2007/2008 - jef.perrin.free.fr