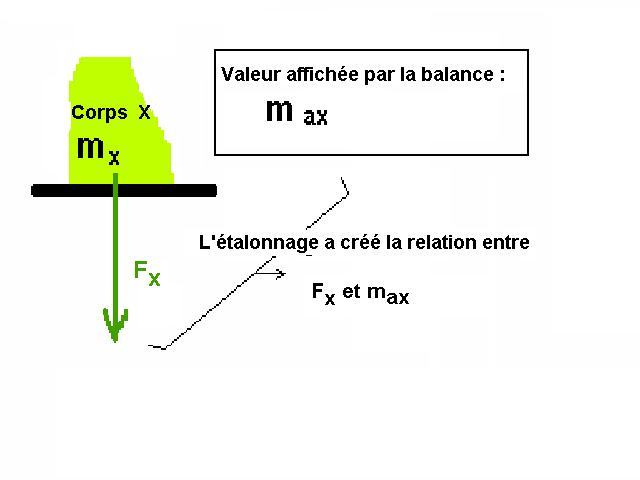
On peut raisonner en considérant la force F que tout corps à peser applique sur le plateau de charge de la balance.
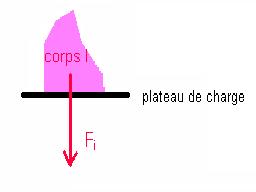
force exercée sur plateau par un corps I

Soit Fi la norme de cette force pour un corps I de masse mi et de masse volumique ρi. On a :

Fi = mi * g - (mi * ρ a / ρi) * g

Où g désigne la valeur du champ de gravité et ρa la masse volumique de l'air.

Le terme mi * g représente le poids du corps I dans le vide.
Le terme mi * ρ a / ρi * g représente la valeur de la poussée d'Archimède appliquée au corps I par l'air.
On peut aussi écrire :

Fi = mi * g * (1-ρ a / ρi)



Lorsqu'on étalonne la balance, on établit une fonction qui fait en sorte que -quand le plateau de la balance est chargé avec une masse étalon de valeur met et de masse volumique ret = 8000 kg/m3- la force Fet associée engendre l'affichage d'une valeur égale à met. Finalement on peut schématiser l'étalonnage par :

met ------ conduit à ----->Fet ----- qui est transduit par la balance en valeur affichée -----> met

Ainsi, lorsqu'on va peser un corps X de masse vraie mx, le plateau de la balance va être soumis à une force Fx qui va être transduite en une valeur affichée max qui obéit à la fonction d'étalonnge. Ce qui signifie qu'on aura :

Soit ρx la masse volumique du corps X. On a la relation :

Fx = mx * g * (1-ρ a / ρx)


Et l'étalonnage de la balance (en le supposant parfait) donne une relation entre la valeur max à l'affichage et Fx. A savoir :

Fx = max * g * (1-ρ a / ρet)

la valeur affichée max n'est donc pas la valeur vraie de la masse mx du corps X sauf si sa masse volumique est identique à celle des étalons (ρet = 8000 kg/m3 par convention).
max s'appelle masse conventionnelle de X. Et on a un biais dont la valeur est donnée en "croisant" les 2 égalités présentées ci-dessus :

mx * g * (1-ρ a / ρx) = max * g * (1-ρ a / ρet)
Soit :
mx = max [(1-ρ a / ρet)]/ [(1-ρ a / ρx)]

Qui peut s'écrire:

mx = max*[rx /(rx- ra )]* (1-ra/ ret)
cqfd

Note : on suppose que les masses volumiques de l'air et des étalons sont constantes tout au long des étalonnages et des mesures. Ce qu'on peut admettre en travaillant à température constante à 20°C ...