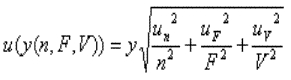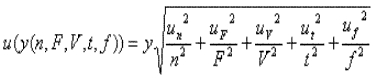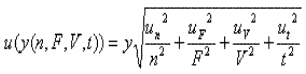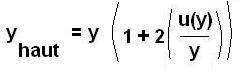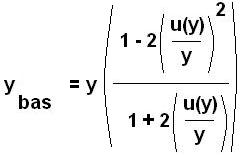Incertitude d'un comptage de particules en chambre de numération

Retour au sommaire du dossier | Retour à l'accueil

Incertitude d'un comptage de particules en cellule de numération

Formule du mesurage :

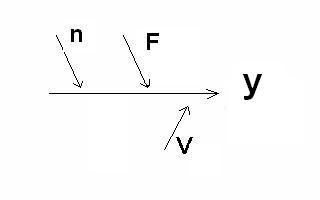
[particules]= y = n F / V

• n : nombre d'éléments comptés ;
• F : facteur éventuel inverse de dilution avant la mise en chambre de numération ;
• V : volume compté ;

C'est la formule du mesurage qui va nous donner le départ pour le recensement des sources d'imperfection (qui peuvent a priori jouer à la fois au niveau d'erreurs systématiques (biais à corriger) et au niveau de l'incertitude). A savoir :

Et ainsi on va commencer le travail en examinant chaque facteur d'influence de près en alliant imagination et une bonne connaissance du processus de mesure ... Il va falloir associer une incertitude-type et éventuellement un facteur de correction à chaque facteur d'influence, puis combiner correctement ces incertitudes-types pour calculer l'incertitude-type globale.
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque n, F et V sont des variables indépendantes.

La loi de propagation des écart-types appliquée au produit de variables indépendantes donnerait alors :

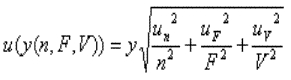
Il s'agirait donc d'estimer u(n), u(V) et u(F)

En fait, si nous regardons maintenant le paramètre n "nombre de particules comptées" (n), les affaires ne sont pas si simples que ça ... et on peut envisager plusieurs problèmes :
- q1 La question de l'aléa fondamental de type "loi de Poisson" sur n (voir plus loin);
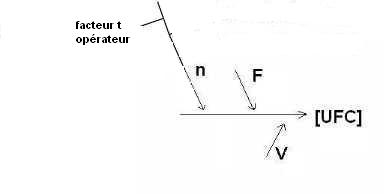
- q2 La question du discernement des particules plus ou moins différent selon les opérateurs : facteur t, t = 1, u_t à déterminer ;
- q3 La question d'une hétérogénéité au départ sur le type d'échantillon : facteur f, f=1, u_f à déterminer ;

Pour ne rien oublier, inscrivons toutes ces nouvelles problématiques dans le "diagramme initial des causes et des effets". On est ainsi conduit à un nouveau diagramme des "causes et des effets" associé à "une nouvelle formule du mesurage".

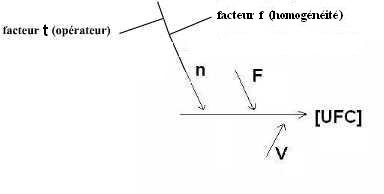
Et on doit modifier la formule du mesurage qui devient :

y = (n F / V) * (t * f)


Et ainsi on va continuer le travail en étudiant chaque "nouvelle" source d'imperfection de près ... Il va falloir associer une incertitude-type et éventuellement une valeur à chaque source, puis combiner correctement ces incertitudes-types pour calculer l'incertitude-type globale.
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque toutes les variables sont indépendantes.

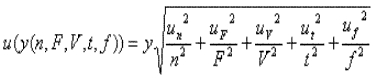
Dans le cadre de cette étude, on va supposer que le facteur f=1 avec une incertitude-type à 0. C'est à dire qu'on suppose que l'échantillon à compter est parfaitement homogénéisable.

Le modèle finalement retenu répond donc au schéma simple suivant :

La formule du mesurage est :

y = (n F t / V)

Et ainsi on va continuer le travail en étudiant chaque "nouvelle" source d'imperfection de près ... Il va falloir associer une incertitude-type et éventuellement une valeur à chaque source, puis combiner correctement ces incertitudes-types pour calculer l'incertitude-type globale.
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque toutes les variables sont indépendantes.

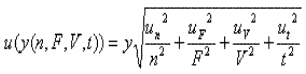
Estimation de u(n)

La distribution de Poisson est souvent la loi de probabilité décrivant les comptes de particules.
Si les particules sont des individus distribués de façon aléatoire dans l'échantillon concerné par le comptage. Et si ces "individus" n'exercent aucun effet de réglage de position les uns par rapport aux autres. Et si le volume global occupé par les particules est faible devant le volume total de l'échantillon (disons moins de 0,5% , mais voir le lien ci-dessous pour des précisions indispensables). Alors on s'attend à une distribution de Poisson pour des comptes répétés.
(cliquer ici pour des justifications concernant l'utilisation d'une loi de Poisson et les conditions limites de cette utilisation)

Soit P(n) la probabilité de trouver n :

P(n)= (mⁿ e^-m)/ n!    avec m moyenne des comptes. La variance est égale à la moyenne m.

Dans le cas d'espèce qui nous intéresse, si on suppose les critères d'utilisation de la loi de Poisson remplis (voir le lien ci-dessus), n, est la meilleure estimation disponible de la moyenne et sera donc utilisé comme estimation de variance. On aura u(n) = √(n).

Evidemment, plus n est grand, plus u(n) est grand mais plus u(n)/n est faible ! Et c'est ça qui importe.

Estimation de u(V)

Il va falloir utiliser les données fabricant sur la chambre de numération. Par exemple pour une chambre de Malassez standard, les fabricants annoncent ± 2 % sur le volume. Soit V à ± (2*V/100).

On utilisera la distribution rectangulaire et donc u(V)=(2*V/100)/√3

Estimation de u(F)

Calcul à conduire en utilisant les données de "comment obtenir l'incertitude-type sur un facteur inverse de dilution". Consultez le lien, calculez puis refermez. Vous aurez besoin de connaître les caractéristiques métrologiques de votre "verrerie".

Estimation de u(t)

Pour cette estimation, il n'y a qu'une étude statistique qui peut nous donner des informations (nous ferons ainsi appel à une estimation dite de type A). Il s'agira de faire compter le même montage final sous microscope (aucun déplacement évidemment) par le plus possible de techniciens confirmés.

Déclinaison sur un exemple pratique

Données de départ :

• Comptage sur la totalité d'une chambre de Malassez. V= 1 µL ±2%. Soit u(V)= (1*2/100)/√3 = 0.012 µL.

• Nombre de "particules" (cellules par exemple !) comptées n = 233. Soit u(n) = √233 = 15.

• Une étude statistique d'effet opérateur a été conduite sur la totalité d'une chambre de Malassez chargée avec environ 200 particules environ et on a obtenu un écart-type de 3,3 en % sur ce comptage par 14 techniciens différents. Soit t=1 et u(t)=0,033.

• Dilution inverse = F = 100 par (50 µL + 4950 µL de diluant) avec des pipettes mécaniques à piston conformes aux normes ISO 8655. Soit pas de biais supposé en moyenne sur les volumes et u(50µL) = 0,5 µL et u(4950µL) = 22 µL. On obtient alors F=100 et u(F)=1,1.
• y = nF/V = 233*100/1 = 23 300 part./µL.

Note : calcul conduit selon "comment obtenir l'incertitude-type sur un facteur inverse de dilution". Consultez, calculez puis refermez.

y = 23,3 10³ particules/µL

Variables

valeurs x_i

incertitude-types u(x_i)

(u(x_i) / x_i)²

Incertitude-type composée

V

1

0,012

(0,012/1)²
=0,000144

le terme en V est quasi négligeable devant les termes en n et t

n

233

15

(15/233)²
=0,00414

F

100

1,1

(1,1/100)²
=0,000121

le terme en F est quasi négligeable devant les termes en n et t

t

1

0,033

(0,033/1)²
=0,00109

le terme en t représente environ le 1/4 du terme en n

On calcule la racine carré de la somme des (u(x_i) / x_i)² et on multiplie par y -->

u(y) = 0,0741 * 23 300 = 1,7₃ 10³ part/µL

Se pose alors la question du facteur d'élargissement à appliquer pour obtenir une incertitude élargie U(y) à la confiance 0,95. En effet, la distribution de Poisson étant la composante majoritaire de l'incertitude-type, l'intervalle de confiance n'est pas, a priori, symétrique avec k=2 selon une loi normale.

On a alors deux possibilités éventuelles ou une...ou trois ...

Si n est grand (par exemple dès 100), on se rapproche dangereusement de la loi normale, et puis y'a aussi la composante t qui normalise. Alors on ose, on applique k=2 pour une confiance à 0,95. Ce qui donne dans notre cas : y = (23,3 ± 3,5) 10³ particules/µL (k=2). Qu'on pourra écrire : y = (24 ± 4) 10³ particules/µL (k=2).

Ou alors, quelque soit n, on applique la formule d'approximation de l'intervalle 0,95 qui a été établie par modélisation des effets de la loi de Poisson combinée à l'effet procédural normal. La Littérature (Seppo I. Niemelä, Publication J4/2003, Centre for metrology and accerditation, Helsinki) donne les formules empiriques d'approximation :

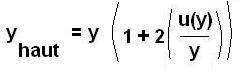y_hte = 23,3 10³*(1 + 2*(1,7 / 23,3)) = 26,7 10³ particules/µL

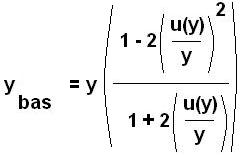y_{limite basse} = 23,3 10³*(1-2*(1,7/23,3)²)/(1 + 2*(1,7/23,3))

= 20,1 10³ particules/µL

Ou alors, à la condition fondamentale que n ait été le facteur ultra majortaire d'incertitude (ce qui n'est pas vraiment le cas puisque le facteur opérateur t conduit à une incertitude-type qui n'est pas si négligeable que ça devant l'incertitude-type sur n), on aurait pu regarder avec un tableur ce que donne le calcul cumulatif des probabilité en loi de Poisson :

P=Σ((nⁱ e^-n)/ i!) de i=0 à l'infini (pas trop loin ...)
et chercher à trouver les valeurs de i qui donnent P#0,025 et P#0,975 (bilatéral 0,95).
A réserver aux petites valeurs de n pour ne pas exploser son tableur (<100). Mais aux trop petites valeurs de n, la confiance sur n comme bonne estimation de la variance de n est d'une précision relative faible et donc critiquable !! On évite de compter en dessous de 50 !

Retour au sommaire du dossier | Retour à l'accueil | Droits de copie | A propos de l'auteur | JF Perrin - 2007 - jef.perrin.free.fr

y = 23,3 10³ particules/µL
Variables	valeurs x_i	incertitude-types u(x_i)	(u(x_i) / x_i)²	Incertitude-type composée
V	1	0,012	(0,012/1)² =0,000144	le terme en V est quasi négligeable devant les termes en n et t
n	233	15	(15/233)² =0,00414
F	100	1,1	(1,1/100)² =0,000121	le terme en F est quasi négligeable devant les termes en n et t
t	1	0,033	(0,033/1)² =0,00109	le terme en t représente environ le 1/4 du terme en n
On calcule la racine carré de la somme des (u(x_i) / x_i)² et on multiplie par y -->				u(y) = 0,0741 * 23 300 = 1,7₃ 10³ part/µL

	y_hte = 23,3 10³(1 + 2(1,7 / 23,3)) = 26,7 10³ particules/µL
	y_{limite basse} = 23,3 10³(1-2(1,7/23,3)²)/(1 + 2*(1,7/23,3)) = 20,1 10³ particules/µL