Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2020
[A propos de l'auteur]
[Droits de copie]
Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2020
[A propos de l'auteur]
[Droits de copie]
La progression est organisée autour d'exercices pratiques.
Le contenu couvre le programme du BTS biotechnologies.
Soit une distribution de n valeurs yi. On peut les organiser pour les représenter en histogramme de distribution.
Pour cela il faut :
Voici un exemple.
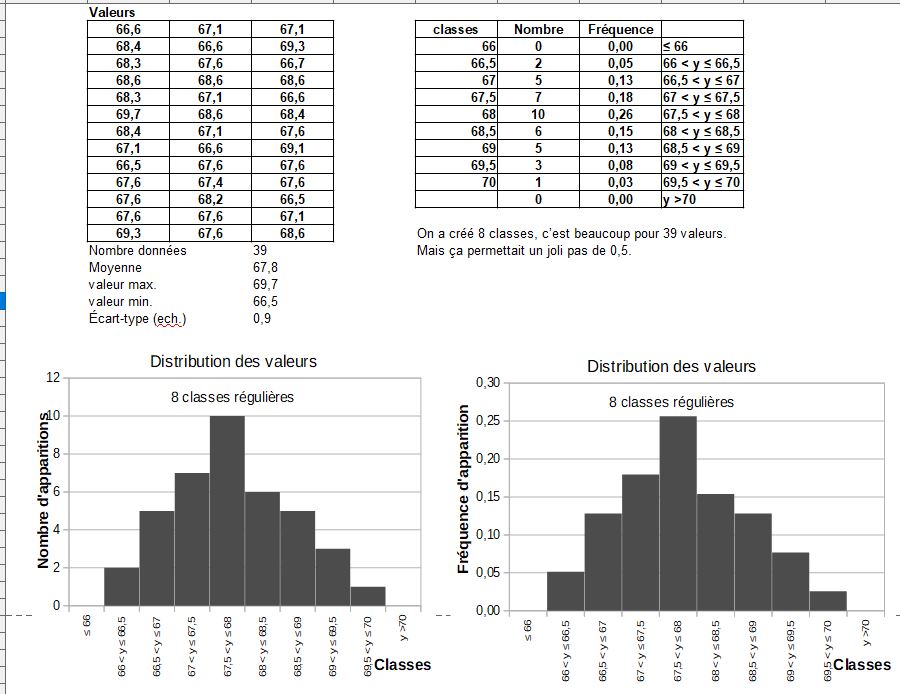
On suppose une distribution n valeurs yi.
Les valeurs collectées concernent la population entière |
Les valeurs collectées sont un échantillon |
| $$ moyenne = \overline{y}=\cfrac { \sum\limits_{n=1}^{n} {y_i}} {n} $$ |
Si les n valeurs collectées ne sont qu'un échantillon d'une population (qui peut être infinie), la moyenne des valeurs collectées n'est qu'une estimation de la moyenne de la population $$ Estimation~de~moyenne = \overset {\sim}{y}=\cfrac { \sum\limits_{n=1}^{n} {y_i}} {n} $$ |
| $$
variance = V(y) = \cfrac {1} {n} \sum\limits_{n=1}^{n} {(y_i - \overline {y})^2}
$$
La variance est un indicateur de dispersion des valeurs : elle est toujours positive, ne s’annule que pour une série statistique dont tous les termes ont la même valeur, est d’autant plus grande que les valeurs sont étalées et est invariante par ajout d’une constante. Et elle a l'avantage d'être cumulative (voir ci-après). Fonction VAR.P avec un tableur. |
Si on a un échantillon et que la moyenne de la population n'est pas connue, c'est à dire qu'on ne connaît qu'une estimation de la moyenne grâce à l'échantillon alors : $$ Estimation~non~biaisée~de~variance \\ = \overset {\sim} {V(y)} = \cfrac {1} {n-1} \sum\limits_{n=1}^{n} {(y_i - \overset {\sim} {y})^2} $$Fonction VAR avec un tableur. |
|
$$
Ecart-type = \sigma = \sqrt {V(y)} = \sqrt {\cfrac {1} {n} \sum\limits_{n=1}^{n} {(y_i - \overline {y})^2}}
$$
L'écart-type est l'indicateur de dispersion le plus "parlant" car il s'exprime dans l'unité des valeurs de la série statistique. Attention. Dès qu'on a des calculs à réaliser, faut travailler avec les variances (faciles à combiner) et seulement en fin de calculs passer en écart-type. Fonction ECARTYPE.P avec un tableur. |
$$
Estimation~non~biaisée~d'écart-type \\ = s = \sqrt { \overset {\sim} V(y)} =
\sqrt {\cfrac {1} {n-1} \sum\limits_{n=1}^{n} {(y_i - \overset {\sim} {y})^2}}
$$
Fonction ECARTYPE avec un tableur. |
On doit souvent combiner des variables aléatoires. On retiendra :
Si on imagine un histogramme avec énormément de valeurs, on pourrait construire un histogramme en fréquence avec un nombre immense de classes qui couvriraient des intervalles tout petit. Si on s'imagine tendre vers l'infini (et au-delà) on "voit" que l'histogramme va tendre vers une courbe "lisse" : on des probabilité sur ℜ.
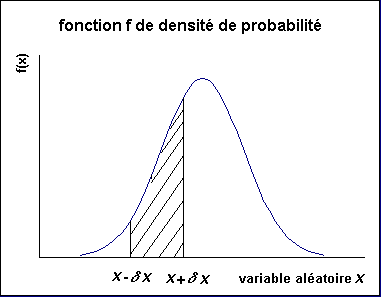
la fonction densité de probabilité s'utilise et se "visualise" ainsi (et c'est fondamental de bien le comprendre) |
|
| Soit p(x,δx) la probabilité que la variable aléatoire soit située entre x - δx et x + δx ; on a : $$ p(x,\delta x) = \int_{x-\delta x}^{x + \delta x} f(x) dx $$ |
 |
|
La surface de la zone en hachurée sur le schéma représente la probabilité
que la variable x soit comprise entre x + δx et x - δx. |
|
La loi de distribution normale (Laplace et Gauss) est la distribution sur ℜ à connaître ! Elle est symétrique centrée sur sa moyenne et on ne peut pas ne pas savoir que l'intervalle moyenne ± 2 écart-type correspond à une probabilité de 0,95. (La valeur exacte n'est pas 2 mais 1,96 ...).