Energie des photons U.V. et visibles et transitions énergétiques

Forme différentielle de la loi de Beer Lambert et un peu plus ; pour ceux qui veulent quelques justifications supplémentaires

L'idée de départ est celle d'une relation différentielle de décroissance linéaire. Du grand classique...
Soit P la puissance radiante incidente éclairant un élément de surface de l'échantillon et l le trajet optique :
$$ dP=-kcPdl $$ où k est le coefficient spécifique de décroissance lié à la substance absorbante en solution et c sa concentration.

Soit :$\frac{dP}{dl} \frac{1}{P}=-kc$ qui s'intègre facilement en :
$$P_t=P_i e^{-klc}$$
en appelant P_t la puissance radiante récupérée (transmise) au bout d'un trajet optique de longueur l et P_i la puissance radiante incidente au départ (pour l=0).

On a obtenu ci-dessus une écriture "naturelle", avec la fonction exponentielle, de la loi de Beer Lambert. Et cette "écriture naturelle" n'est pas utilisée, mais on lui préfère l'écriture équivalente en puissance de 10, à savoir :
$$P_t=P_i 10^{-\varepsilon lc}$$ qui donne le célèbre $A=\varepsilon lc$ avec $A =\log_{10} \left ( \frac{P_i}{P_t} \right )$

Remarque au sujet du passage de la forme exponentielle à la forme en puissance de 10 : comme 10^x = e^xln10 on a k=εln10.

Reste désormais à s'intéresser à la propriété d'additivité qui se déduit facilement à l'aide de petits calculs.

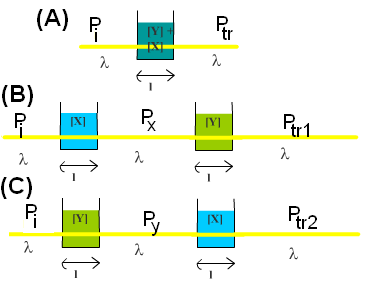• En (A) : $ dP=-k_x[X]Pdl -k_y[Y]Pdl = -(k_x[X]+k_y[Y])Pdl $ qui s'intègre en $ P_{tr}=P_i e^{-(k_x[X]+k_y[Y])l} = P_i {e^{-k_xl[X]}}e^{-k_yl[Y]} $

Donc avec l'écriture en "puissance de 10", en (A) on obtient : $ P_{tr}=P_i {10^{-\varepsilon_xl[X]}}10^{-\varepsilon_yl[Y]} $).

• En (B) : la loi de Beer lambert appliquée à la première cuve donne $ P_x=P_i 10^{-\varepsilon_x l[X]} $. On applique à nouveau la loi de Beer Lambert pour la deuxième cuve et on obtient, puisque le flux transmis de la première cuve est le flux incident de la deuxième cuve : $ P_{tr1}=P_i 10^{-\varepsilon_x l[X]}10^{-\varepsilon_y l[Y]} $

• On applique en (C) le même raisonnement qu'en (B) pour obtenir : $ P_{tr2}=P_i 10^{-\varepsilon_y l[Y]}10^{-\varepsilon_x l[X]} $.

• On a ainsi montré que : $ P_{tr}=P_{tr1}= P_{tr2}=P_i 10^{-\varepsilon_x l[X]}10^{-\varepsilon_y l[Y]} $.

Soit : $ A=\log_{10} \left ( \frac{P_i}{P_{tr}} \right ) = {\varepsilon_x l[X]}+{\varepsilon_y l[Y]} $. CQFD.

retour en haut de page