Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2004/2013
[A propos de l'auteur]
[Droits de copie]
On se contentera du schéma de principe ci-dessous (qui n'est absolument pas un schéma de construction) :
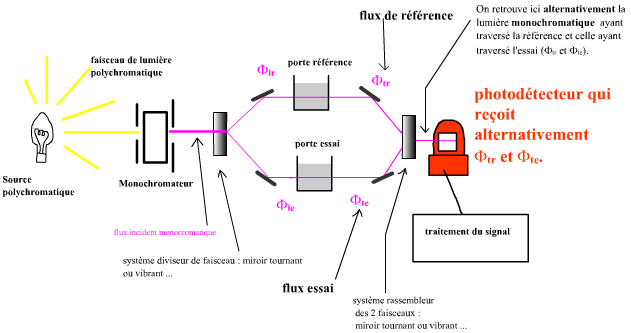 |
L'appareil mesure Φtr et Φte alterntivement. ( t pour transmis, r pour référence , e pour essai).
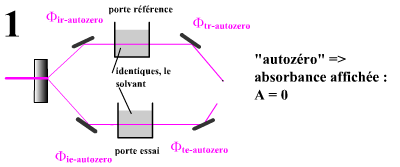
Dans un premier temps, il va falloir équilibrer les flux de référence et essai : c'est la tâche de la fonction "autozéro".
L'autozéro est réalisé en ne plaçant aucune cuve échantillon au niveau de la cuve de référence et de la cuve essai (autozéro contre l'air) ou en plaçant deux cuves identiques chargées en solvant dans le porte échantillon de référence et d'essai.
 |
Sur les appareils anciens, l'équilibrage s'effectuait de façon optique : un coin optique permettait d'équilibrer le diviseur de flux de la source et d'obtenir exactement Φtr-autozero = Φte-autozero. Sur les appareils récents, l'autozéro est réglé de façon "informatique". La division
équilibrée du flux source en 2 flux incidents n'a pas besoin d'être parfaite. Il suffit à l'appareil
de déterminer la valeur |
Une fois l'opération "autozéro" réalisée, l'appareil pourra être utilisé pour des mesures.
Comme on va le montrer ci-dessous, le spectrophotomètre bifaisceaux ne mesure que des différences d'absorbance : la différence d'absorbance entre un échantillon qui sera utilisé comme référence et placé dans le porte échantillon de référence et un échantillon placé dans le porte échantillon essai.
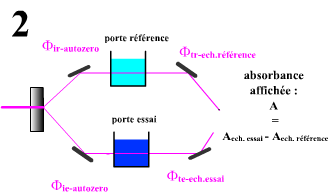 |
L"autozéro" réalisé, on peut désormais lire les échantillons essais
à mesurer contre l'échantillon de référence choisi. Compte tenu de sa construction, il va afficher :
Aaffichée Voir la démonstration rigoureuse ci-dessous ... |
|
En fait, l'appareil affiche comme absorbance mesurée : Aaffichée = Log(Φtr-ech.référence / Φte-ech.essai)- Log(r). (où r désigne le décalage des flux mesuré lors de l'autozéro, voir §2.1) Comme : Log(Φtr-ech.référence / Φte-ech.essai)- Log(r) = Log[(Φtr-ech.référence / Φtr-autozéro)* (Φtr-autozéro / Φte-autozéro)* (Φte-autozéro / Φte-ech.essai)- Log(r) On peut écrire : Aaffichée = Log(Φtr-ech.référence / Φtr-autozéro) + Log(Φtr-autozéro / Φte-autozéro) + Log(Φte-autozéro / Φte-ech.essai) - Log(r) Soit : Aaffichée = Log(Φtr-ech.référence / Φtr-autozéro) + Log(Φte-autozéro / Φte-ech.essai) puisque Log(Φtr-autozéro / Φte-autozéro) = Log(r) Soit : Aaffichée = Log(Φte-autozéro / Φte-ech.essai) - Log(Φtr-autozéro / Φtr-ech.référence) (formule "f") Or : Log(Φte-autozéro / Φte-ech.essai) représente très exactement la composante d'absorbance due à la solution essai présente dans la cuve du porte cuve essai et Log(Φtr-autozéro / Φtr-ech.référence) la composante d'absorbance due à la solution de référence présente dans la cuve du porte cuve de référence D'où : Aaffichée = (Absorbance cuve essai - Absorbance cuve de référence) |
|
Contrairement à ce qui se passe avec un appareil monofaisceau, une condition essentielle à la qualité des mesures n'est plus la stabilité absolue de l'énergie délivrée par la source tout au long des mesures. Si la source fluctue de manière lente devant la fréquence des mesures alternée référence/essai, il n'y a aucun problème !
( Pour en avoir le coeur net, introduisez un facteur de fluctuation f dans la formule "f" de la démonstration ci-dessus. Vous allez devoir introduire f à la fois au niveau de Φte-ech.essai et Φtr-ech.référence. Comme Log(a*b) = Log(a)+ Log(b), il va disparaître ...essayez).
On peut aussi signaler que les mesures ne sont pas entachées des éventuelles fluctuations de réponse du photomultiplicateur ( si ces dérives sont lentes devant la fréquence des mesures alternée référence/essai).
Le montage bifaisceaux est propice à l'étude de spectres. En effet, la construction même de
l'appareil le rend insensible aux 2 phénomènes suivants :
- l'éclairement incident dépend de la longueur d'onde (les sources ne donnent pas la même énergie à toutes les longueurs d'onde)
. (Aisé à démontrer en s'inspirant du paragraphe 1.2);
- la réponse des photomultiplicateurs dépend elle aussi de la longueur d'onde. Le montage de
l'appareil en 2 faisceaux séparés sur la mesure et la référence rend la mesure d'absorbance indépendante
des variations de réponse du photomultiplicateur.
Pour obtenir un spectre, après réalisation de l'"autozéro" à une longueur d'onde donnée, il suffira
de demander un balayage de longueurs d'onde au monochromateur.
Avant l'informatisation des spectrophotomètres monofaisceaux et l'apparition des capteurs barettes de diode ou CCD, avancées techniques qui les a rendu aptes
à la réalisation rapide de spectres, les montages bifaisceaux étaient vraiment avantageux !
On se contentera du schéma de principe ci-dessous :
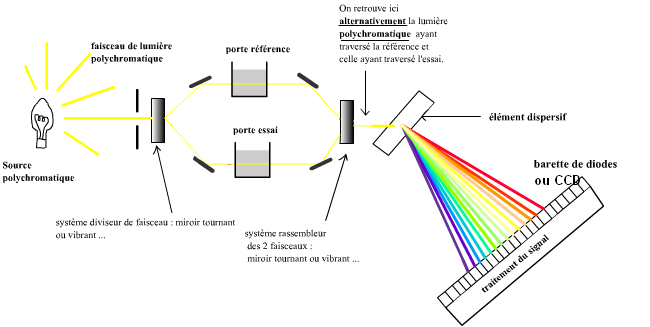
Le porte référence et le porte essai reçoivent alternativement le flux incident de lumière polychromatique. L'élément dispersif est situé après et reçoit alternativement le flux transmis polychromatique issu de la référence et de l'essai (grâce au miroir tournant rassembleur). Finalement, chaque photodiode de la barette reçoit alternativement une bande passante étroite de longueur d'onde (monochromatisme) issue alternativement de la référence et de l'essai. Ainsi chaque photocapteur de la barette permettra finalement une mesure à une λ donnée (en fait avec une largeur de bande passante donnée). La fonction "autozéro" réalisera chaque "autozéro" valable pour chaque photocapteur. Finalement on pourra avoir les mesures d'absorbances contre la référence pour toutes les λ autorisées par la source en simultané ! = mesures multilongueurs d'onde en simultané ! Et ceci avec les avantages du montage en double faisceau, à savoir la non sensibilité à l'instabilité de la source et aux dérives de la photoréception.