Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour sept. 2016
[A propos de l'auteur]
[Droits de copie]
Les échanges, les transformations liées aux activités du vivant sont évidemment soumis au principe de conservation de l'énergie et au principe de l'accroissement global de l'entropie.
Selon le premier principe de la thermodynamique, l'énergie n'est ni créée ni détruite mais convertie sous ses différentes apparences. Par exemple lors de la photosynthèse, les plantes vertes convertissent de l'énergie photonique en énergie potentielle de liaisons covalentes retrouvées dans le glucose ou l'amidon synthétisés à partir du dioxyde de carbone. Dans toutes les cellules du vivant l'énergie potentielle de liaisons covalentes peut être convertie vers un potentiel électrique de membrane ou un gradient de concentration trans-membranaire. Et évidemment aussi en chaleur.
Les systèmes biologiques fonctionnent généralement à température (T) et pression (P) constantes. Dans de tels systèmes, une fonction d'état thermodynamique
appelée énergie libre de Gibbs (G) permet de prédire la spontanéité d'une réaction chimique. Soit envisagée une transformation d'un état A vers un état B :
• si ΔG < 0 (réaction exergonique), la spontanéité mène le système de A vers B.
• si ΔG> 0 (réaction endergonique), la spontanéité conduit le système de B vers A.
• si ΔG= 0, le système est à l'équilibre.
Attention. Le fait qu'un processus puisse être qualifié de spontané ne signifie pas que le processus se déroule à vitesse importante. La thermodynamique (avec ΔG) renseigne de ce qui est naturellement possible (spontanéité) mais ne dit rien de l'aspect cinétique ! La cinétique sera peut être très rapide ou peut être nulle...
Dans les ouvrages, G est appelé énergie libre de Gibbs ou enthalpie libre ou simplement énergie libre...
On montre qu'à pression et température constante (cas du vivant) ΔG = ΔH - TΔS.
ΔH est la valeur exothermique ou endothermique de la transformation étudiée, ΔS est la valeur de variation entropique de la transformation étudiée, T la température absolue.
Soit le cas de la fusion de la glace : glace -> eau liquide
ΔH vers 5500-6500 J.mol-1 est positif : réaction endothermique, pour passer de la glace à l'eau liquide, il faut casser des liaisons hydrogènes donc "fournir de la chaleur".
Mais ΔS = 22,1 J.K-1mol-1est positif : la réaction est donc favorable d'un point de vue entropique, les molécules d'eau sont plus désordonnées dans l'eau liquide que dans la glace.
Voyons ce que cela donne selon la température à laquelle se trouve l'eau.
Température | ΔH (J/mol) | TΔS (J/mol) | ΔG = ΔH - TΔS | Spontanéité |
10°C = 283,15 K | +6400 | 283,15*22,1 = +6257 | -150 | La glace fond. En fondant, elle "prend de la chaleur" mais c'est plus que compensé par l'effet entropique TΔS |
0°C = 273,15 K | +6037 | 273,15*22,1 = +6037 | 0 | équilibre de l'eau liquide et de la glace : endothermie et effet entropique se compensent exactement |
-10°C = 263,15K | +5600 | 263,15*22,1= +5816 | +180 | La glace ne fond pas à -10°C |
Valeurs données à pression atmosphérique.
On appelle variation d'énergie libre standard à pH 7 et 25°C (notée généralement ΔG0', exprimée en J/mol), la variation de l'énergie libre pour des conditions où la pression est à 1 bar (1000 hPa) et où les réactifs sont à la concentration de 1 mol/L (sauf H3O+ et OH-), le pH à 7, la température à 25°C.
Évidemment, les concentrations dans les systèmes biologiques sont rarement à 1 mol/L ! Et on montre que : $$ \Delta G = \Delta G^{0 \prime} + RT \ln \frac {[C][D]}{[A][B]} $$ (où R est la constante des gaz parfaits en J.mol-1.K-1 et T la température absolue en K)
Une relation fondamentale relie ΔG0 et Keq (constante d'équilibre de la réaction) : $$ \Delta G^{0 \prime} = - RT \ln K_eq $$
Soit CA et CA les concentration d'un même soluté S dans les compartiments A et B

La relation générale est :
$$ \Delta G(J/mol) = RT \ln \frac {[S]_B}{[S]_A} - nF \Delta E$$(où n est la charge unitaire éventuelle du soluté S, F le Faraday et ΔE la différence de potentiel éventuelle de part et d'autre de la membrane EA-EB)
Si le soluté S n'est pas chargé (n=0), on a simplement l'effet gradient de concentration qui détermine ΔG, soit
\( \Delta G(J/mol) = RT \ln \frac {[S]_B}{[S]_A} \)
La spontanéité est un transfert du plus concentré vers le moins concentré. Un cas bien connu !
Si le soluté S est chargé (n≠0), on voit que ΔG a 2 composantes, l'effet gradient de concentration et l'effet du au potentiel de membrane.
Supposons une membrane qui sépare un compartiment extérieur de pH 6 d'un compartiment intérieur de pH 7 et qui présente un potentiel de membrane de 150 mV
entre l'intérieur et l'extérieur (la face extérieure est à +150mV par rapport à la face intérieure). Si les protons peuvent passer la membrane,
la thermodynamique dit qu'ils le feront de l'extérieur vers l'intérieur et par somme de 2 raisons, le gradient de concentration et l'effet différence de potentiel électrique.
A 25°C, le calcul donne ΔG = 8,31*298*ln(10-7/10-6)-1*965000*0,150 = -5700 - 14500 = - 20200 J/mol = -20 kJ/mol. Les protons ont une forte envie de rentrer ! Encore faut-il
qu'un élément de perméabilité rende cette rentrée possible...
Ce qui a été écrit pour les réactions chimiques en 3.1 est évidemment valable mais on peut ajouter la relation entre ΔG et la différence de potentiel redox (ΔE) des couples en jeu : \( \Delta G(J/mol) = - nF \Delta E \)
Il est intéressant de rappeler que le sens spontané de transfert des électrons est d'aller vers les potentiels positifs (les électrons vont du pôle - au pôle +). Ainsi dans une réaction redox, les électrons sont transférés depuis le réducteur du couple le plus réducteur (potentiel redox le plus faible, le pôle-) vers l'oxydant du couple redox le plus oxydant (potentiel redox le plus fort, le pôle+).
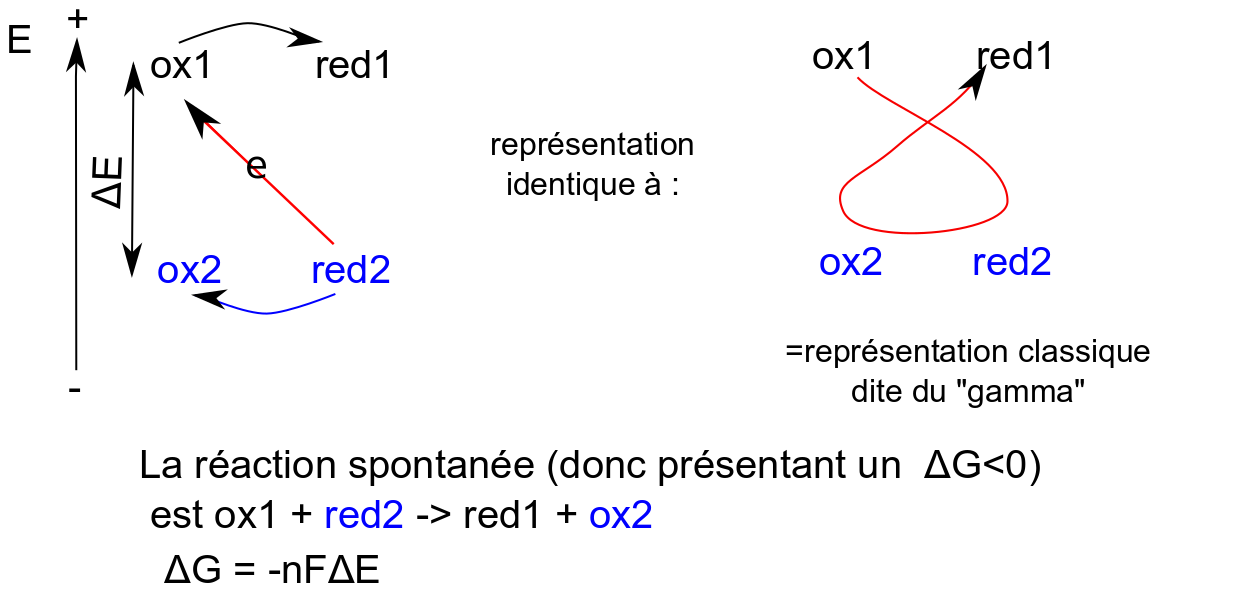
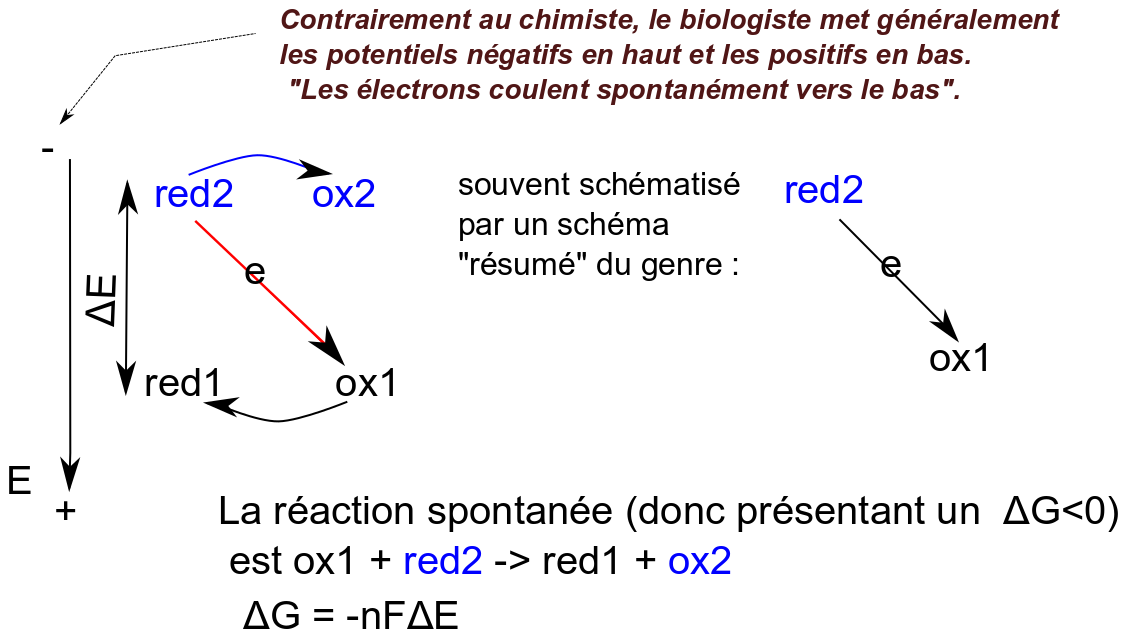
Remarque importante. Dans la plupart de leurs représentations les biologistes "aiment" que le sens spontané des électrons soit représenté dans le sens descendant. C'est assez suggestif de la spontanéité : spontanément l'eau coule vers le bas, une centrale hydroélectrique va utiliser l'énergie de l'eau qui va de haut en bas pour la convertir en électricité... Ainsi les schémas redox biologiques sont-ils généralement représentés ainsi :
Et on rappelle la relation de Nernst pour calculer le potentiel d'équilibre d'un couple redox a Ox + n e / b Red : $$ E = E^0 + \frac {RT}{nF} \ln \frac {[Ox]^a}{[Red]^b} $$
Soit "à réaliser" la transformation (1) A + B -> C + D et ΔG1 > 0
Cette transformation est thermodynamiquement impossible.
Soit la réaction (2) X -> Y avec une thermodynamique favorable ΔG 2 < 0
Soit ΔG1 + ΔG2 < 0
Alors, la réaction A + B + X -> C + D + Y a pour ΔG ΔG=ΔG1 + ΔG2 < 0 et donc une spontanéité thermodynamique favorable.
Attention, il faut bien avoir en tête que A + B -> C + D reste impossible ! On y va par un autre chemin qui va faire appel à un intermédiaire commun entre 2 réactions (le couplage) et c'est cet autre chemin, qui rend 2 réactions solidaires, qui est thermodynamique favorable.
Ci-dessous un lien vers une image illustrant la notion de couplage avec une image mécanique (http://cbc.arizona.edu/classes/bioc462/462a/NOTES/Bioenergetics/Fig1_9aFreeEnergyCoupMech.GIF, Department of Biochemistry and Molecular Biophysics The University of Arizona):
Ci-dessous une exemple plus biochimique de couplage qui illustre que la réaction couplée n'est pas une juxtaposition de 2 réactions mais une nouvelle réaction et qui illustre la notion d'intermédiaire commun dans un couplage :
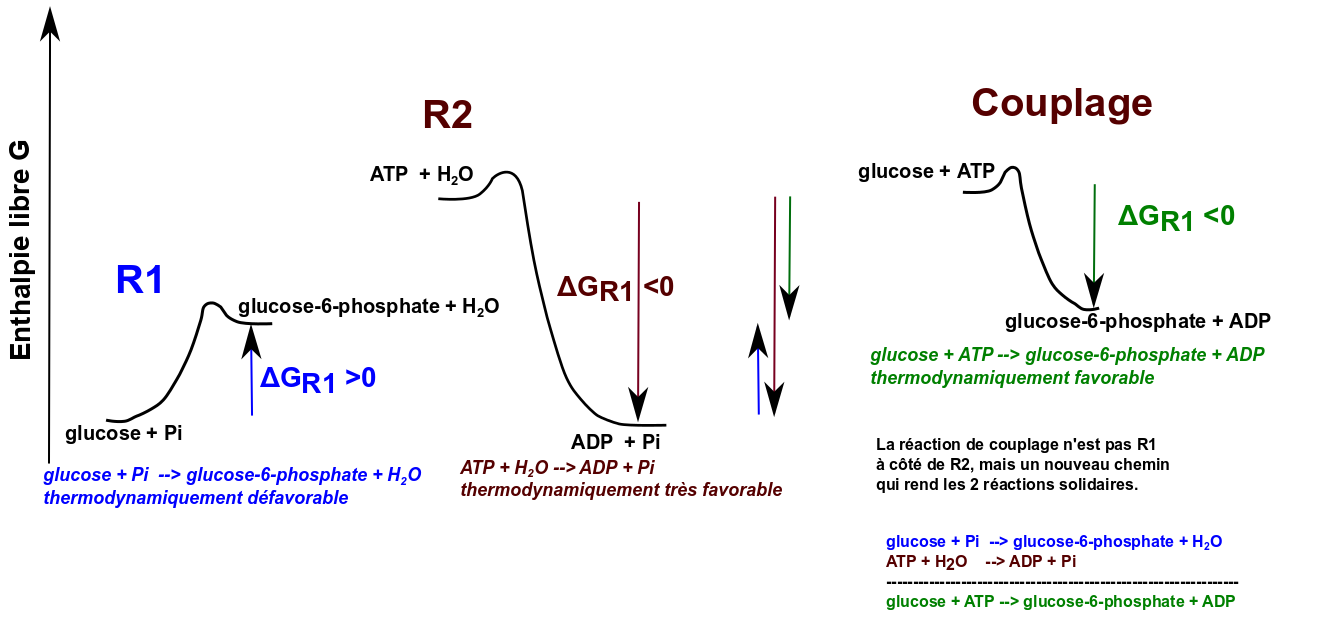
Dans le cas des systèmes vivants (cas où on ne rencontre pas de machines thermiques complexes avec plus d'une source de chaleur), le travail utile qu'une transformation peut céder est borné par la variation d'enthalpie libre au cours de la transformation. Autrement dit, il n'existe pas d'échange avec un rendement en travail utile à 100%, il y aura forcément des pertes en chaleur.