Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2020
[A propos de l'auteur]
[Droits de copie]
![]()
Le test de Mann - Whitney est aussi appelé test de Wilcoxon - Mann - Whitney, du nom des inventeurs.
Il s'agit de comparer 2 échantillons indépendants (non appariés) de valeurs quantitatives en posant comme première intention l'hypothèse nulle, H0 :
"Nous n'apportons pas la preuve d'une différence, la différence constatée peut s'expliquer simplement par les facteurs aléatoires (variables parasites,
facteurs aléatoires ...)".
C'est un test au fonctionnement très classique : à partir des données le test propose de calculer la valeur d'une variable de décision. Puis on va appliquer une règle de décision : on va mettre en relation la valeur calculée à partir de nos données avec la loi statistique qui va nous donner la probabilité que cette valeur soit dépassée ( plus grande ou plus petite) dans le cadre de l'hypothèse nulle (par le seul aléa d'échantillonnage). Si la probabilité trouvée (p) est très faible, on rejettera l'hypothèse nulle au risque p de se tromper. Si la probabilité (p) n'est pas faible, on ne rejettera pas l'hypothèse nulle : on dira qu'on n'a pas montré de différence significative. Évidemment, quelle que soit la conclusion on prend un risque de se tromper !
Le test de Mann-Whitney, qui repose sur la notion de rang, n'exige aucune propriété sur les lois de probabilités que pourraient suivre les variables considérées (en particulier pas d'hypothèse de normalité). Il est ainsi qualifié de non paramétrique. Ce test est bien adapté à la comparaison d'échantillons de faibles effectifs. Il est très utilisé en biologie. Il teste les rangs des valeurs d'une variable V dans un échantillon Ech-A (n valeurs xi) face à un échantillon Ech-B (m valeurs yi). Sous l'hypothèse nulle H0 les 2 échantillons sont issus de la même population (infinie) et P(xi > yi) = P(xi < yi).
❘ H0 : Les 2 échantillons sont issus de la même population parente (infinie).
❘ H1 : Les 2 échantillons ne sont pas issus de la même population parente, il y a une différence de rangs moyens.
Soit F1(V) la fonction de répartition de V dans une population A et soit F2(V) la fonction de répartition de V dans une population B.
\( H0~:~F1(V)=F2(V) \\ H1~:~(F1(V)\prec F2(V))~~ou~~(F1(V) \succ F2(V)) ~~(test~bilatéral)\\ où~~ \prec~et~\succ~renvoient~à~un~effet~sur~le~rang~moyen \)Très souvent, on peut travailler avec l'hypothèse que les fonctions de répartition de la variable V dans les 2 populations étudiées ont la même forme et que si elles diffèrent, elles ne diffèrent que par décalage. Le test peut alors s'écrire comme présenté juste ci-dessous.
Les hypothèses du test sont, dans le cadre de fonctions de même forme :
\( H0~:~F1(V)=F2(V+\theta)~~~\theta = 0 \\ H1~:~F1(V)=F2(V+\theta)~~~\theta \ne0~~(test~bilatéral) \\ où~~ \theta~est~le~décalage~entre~les~fonctions \)Dans toute la suite de ce chapitre, on considère qu'on travaille avec des distributions de même forme. Si ce n'est pas le cas, il faut se contenter donc d'une conclusion en "rangs moyens qui diffèrent significativement ou pas" et l'interprétation du test de Mann-whitney devient ainsi beaucoup plus délicate et complexe. Voici un lien vers un bref article illustrant cette complexité : Hart A. Mann-Whitney test is not just a test of medians: differences in spread can be important. BMJ. 2001;323(7309):391-393. doi:10.1136/bmj.323.7309.391 à l'adresse https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1120984/ .
Soit un lot A (n=10 valeurs xi) et un lot B (m=10 valeurs yi) mesurés pour la grandeur G
Lot A |
7,6 |
9,0 |
8,2 |
8,5 |
8,8 |
7,4 |
5,8 |
7,8 |
8,7 |
6,9 |
Lot B |
10,3 |
9,8 |
8,5 |
7,4 |
7,7 |
9,2 |
6,6 |
10,1 |
8,9 |
10 |
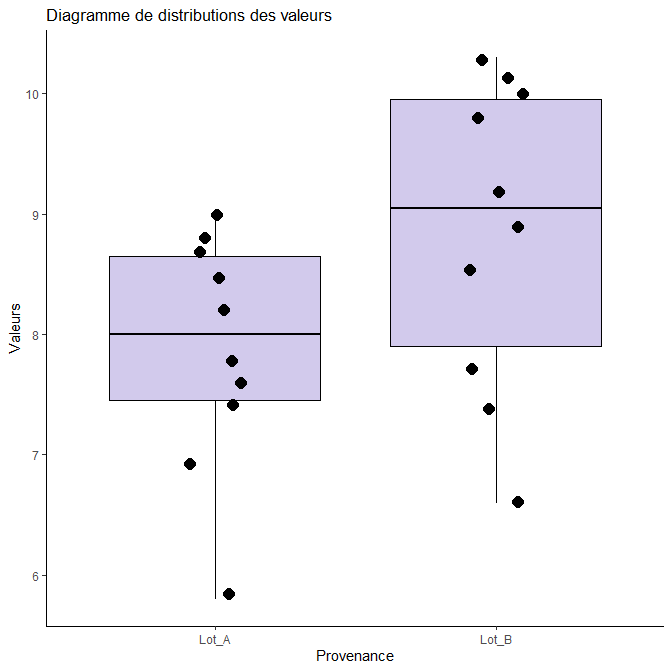
Peut-on considérer que les 2 lots ont des résultats de mesures sans décalage ? décalés ?
Demandons à un connaisseur d'appliquer le test de Mann-Whitney, que va-t-il nous dire :
Il va nous dire :
On va annoncer qu'on n'a pas montré de différence significative entre les 2 lots. On ne rejette pas l'hypothèse HO : "on ne rejette pas que la distribution de la variable quantitative soit la même dans les 2 groupes".
Vous pouvez tester à https://www.socscistatistics.com/tests/mannwhitney/ .
Soit un lot A (n=11 valeurs xi) et un lot B (m=11 valeurs yi) mesurés pour la grandeur G
Lot A |
7,6 |
8,6 |
8,2 |
8,5 |
8,0 |
7,4 |
5,8 |
7,8 |
6,1 |
6,9 |
5,7 |
Lot B |
10,3 |
9,8 |
8,5 |
8,4 |
7,7 |
9,2 |
6,6 |
10,1 |
8,9 |
10,0 |
10,2 |
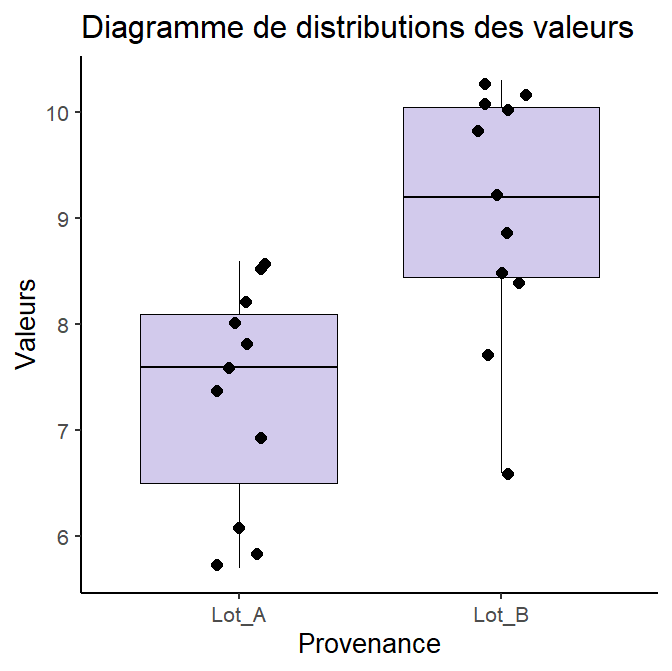
Peut-on considérer que les 2 lots ont des résultats de mesures sans décalage ? décalés ?
Demandons à un connaisseur d'appliquer le test de Mann-Whitney, que va-t-il nous dire :
Il va nous dire :
On peut annoncer qu'on rejette que la distribution de la variable quantitative soit la même dans les 2 groupes" au seuil 0,01 (0,0043) de se tromper.
Le célèbre langage R dit "alternative hypothesis: true location shift is not equal to 0".
Dans les articles c'est la significativité "**" de différence.
Vous pouvez tester à https://www.socscistatistics.com/tests/mannwhitney/ .
Soit un lot A (n=12 valeurs xi) et un lot B (m=10 valeurs yi) mesurés pour la grandeur G
Lot A |
7,6 |
9,0 |
8,2 |
8,5 |
8,8 |
7,4 |
5,8 |
7,8 |
8,7 |
6,9 |
5,7 |
6,1 |
Lot B |
10,3 |
9,8 |
8,5 |
7,4 |
7,7 |
9,2 |
6,6 |
10,1 |
8,9 |
10 |
NA |
NA |
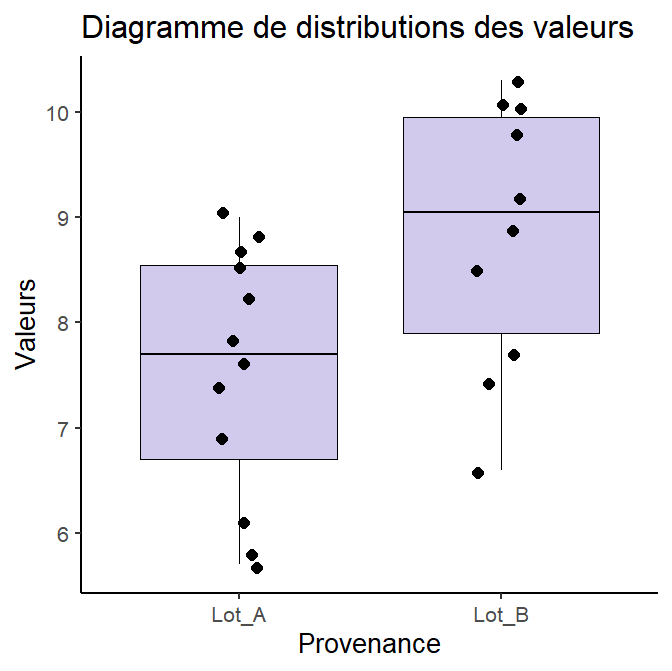
Peut-on considérer que les 2 lots ont des résultats de mesures sans décalage ? décalés ?
Demandons à un connaisseur d'appliquer le test de Mann-Whitney, que va-t-il nous dire :
Il va nous dire :
On peut annoncer qu'on rejette que la distribution de la variable quantitative soit la même dans les 2 groupes" au seuil 0,05 (0,032) de se tromper.
On peut annoncer aussi qu'on ne rejette pas que la distribution de la variable quantitative soit la même dans les 2 groupes au seuil de risque 0,01.
Dans les articles c'est la significativité "*" de différence.
Vous pouvez tester à https://www.socscistatistics.com/tests/mannwhitney/ .