Comment combiner des incertitudes-types

Comment combiner des incertitudes-types dans un calcul global d'incertitude

Soit une grandeur y à mesurer sur un objet O.
Soit x₁, x₂ ... x_i, ... les paramètres qui déterminent y. Ce qu'on écrit y(x₁, x₂ ...).
Soit u(y) noté aussi u(y(x₁, x₂ ...)) l'incertitude-type sur y et u(x_i) l'incertitude-type sur le paramètre x_i.

2. Cas avec variables x_i indépendantes

Les r_i,k sonts nuls, La relation générale vue pour le cas des variables non indépendantes se simplifie en : (attention, la relation qui suit est fondée sur une approximation en série de Taylor du premier ordre de y=f(x_i) autour des espérances mathématiques des x_i)

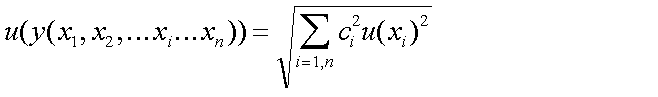
Avec c_i = ∂y/∂x_i. Les c_i sont des dérivées partielles et sont en fait des coefficients de sensibilité. Le produit c_iu(x_i) représente en fait l'incertitude sur y en provenance de l'incertitude sur x_i. Le produit c_iu(x_i) est souvent dénoté u(y,x_i).

Et donc, on voit que les affaires se simplifient par rapport à la formule plus générale précédente !! Mais, il y des cas particuliers pour lesquels tout devient encore plus simple. Et ces cas très simples sont très fréquents ! Vous pouvez les appeler à l'aide du menu de gauche.

(La relation exposée ci-dessus est inapplicable dans les cas où il y a nécessité d'inclure dans la relation des termes d'ordre plus élevé dans le développement en série de Taylor)