Etalonnages avec étalon interne

3. Etude de cas n°3 (dosage en photométrie d'émission atomique de flamme (FEP) avec appareil à double canal)

3.1 Présentation d'un dosage de potassium avec étalon interne lithium

On utilise un photomètre d'émission atomique de flamme à 2 canaux pour doser le potassium déchantillons biologiques liquides. Le faisceau de dosage du potassium est réglé sur les raies 766,5-769,5 du potassium. Le lithium est supposé totalement absent des échantillons à doser (le dosage proposé n'est valable que pour des échantillons dépourvus de lithium !!!). Il est utilisé comme étalon interne. Le canal pour létalon interne est ainsi réglé sur la raie à 671 nm du lithium

3.2 Etablissement d'une fonction d'étalonnage

On va étalonner l'analyse avec une série d'étalons de concentrations variables en potassium mais contenant aussi l'autre étalon -l'étalon interne- en l'occurence le lithium.
On réalise 5 mélanges étalons qui sont mesurés selon les indications du tableau suivant :

	T0	T1	T2	T3	T4	T5
Étalon [KCl] à 5,00 mmol/L en mL	0	1	2	5	15	10
Etalon [LiCl] à 5,00 mmol/L en mL	0	10	10	10	20	10
Eau bidistillée en mL	X	qsp 100 en fj^*	qsp 100 en fj	qsp 100 en fj	qsp 200 en fj	qsp 100 en fj
Emission relative sur le faisceau K	0	40	83	203	307	402
Emission relative sur le faisceau Li	0	198	203	199	201	197

* fj signifie fiole jaugée

Pour chaque signal d'émission potassium mesuré, si l'appareil était "parfait", la valeur du signal (S_et) serait parfaitement proportionnelle à la concentration de l'analyte (c_et)selon un coefficient de réponse caractéristique (k_et) :

c_et = k_et * S_et    (relation (a), appareil idéal)

(Note : cette relation est une donnée de base liée à la technique d'émission atomique de flamme, voir éventuellement un cours à ce sujet)

Pour chaque signal d'émission lithium mesuré, si l'appareil était "parfait", la valeur du signal (S_i) serait parfaitement proportionnelle à la concentration de l'analyte (c_i)selon un coefficient de réponse caractéristique (k_i) :

c_i = k_i * S_i    (relation (b), appareil idéal)

On remarque "malheureusement" que les signaux obtenus pour le lithium sont sensiblement différents alors que la concentration en lithium de tous les étalons est la même. Et ceci au delà des imperfections sur la qualité des pipetages. Ceci est lié à des dérives au niveau de l'appareil : dérives au niveau du débit de nébulisation vers la flamme, dérives de température de flamme, dérives au niveau de la photoréception et de l'amplification ... Les facteurs de réponse sont constants en théorie mais évoluent en fait en fonction des dérives de l'appareillage ... Et c'est bien ce qui nous ennuie a priori pour pouvoir tracer une fonction d'étalonnage de grande qualité avec de simples solutions étalons de potassium!

Cependant pour une injection donnée dans l'appareil "imparfait" mis en oeuvre (on injecte une même solution qui contient le lithium étalon et le potassium étalon), les relations (a) et (b) peuvent être "désidéalisées" par :

c_et = k_et * f * S_et     (où f désigne un facteur lié aux fluctuations et dérives de l'appareillage pour le potassium, f fluctue de façon inconnue)

c_i = k_i * f' * S_i     (où f' désigne un facteur lié aux fluctuations et dérives de l'appareillage pour le lithium, f' fluctue de façon inconnue)

Etablissons le rapport de ces 2 égalité, on obtient :
c_et / c_i = (k_et / k_i) * (f/f') * (S_et / S_i)

Si on admet que f/f' est constant pour une série de mesures, c'est à dire que les fluctuations et les dérives touchent à l'identique les 2 canaux de mesure potassium et lithium. Et ceci est vrai si on se réfère à la construction des photomètre d'émission atomique de flamme bifaisceaux. Alors on peut dire que (k_et / k_i) * (f/f') est constant dans une série de mesures.

Voilà donc la relation d'étalonnage intéressante et c'est :
(S_et / S_i) est proportionnel à (c_et / c_i)

On se livre aux calculs, on trace (S_et / S_i) = f( (c_et / c_i) ; et on obtient :

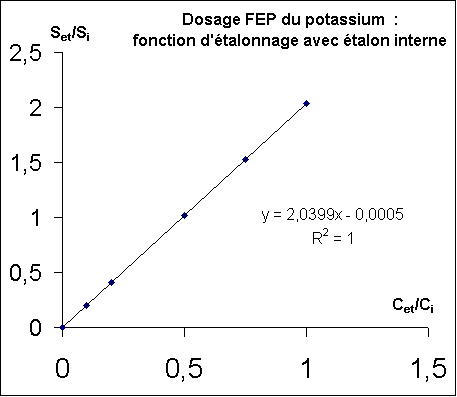Pour construire le graphe présenté on a exprimé les concentrations potassium et en lithium dans les diverses solutions étalons selon les données du tableau de résultats précédent.
L'équation de la droite de régression figure sur le graphe accompagnée de son coefficient de corrélation.
Elle est désormais considérée comme la fonction d'étalonnage

3.3 Mesure d'un échantillon donné

Un essai est réalisé ainsi : on ajoute 10,00 mL dune solution étalon de lithium à 5,00 mmol/L à 90,00 mL déchantillon à doser (grâce à un ajustage en fiole jaugée). On obtient une émission de 199 pour le canal lithium et de 197 pour le canal potassium.

Le rapport des signaux est de 0,98995. La fonction d'étalonnage associe cette valeur à un rapport de concentration du potassium au lithium de 0,4855.
La concentration en lithium dans l'essai analysé était de 500 µmol/L. On en déduit donc une concentration en potassium dans l'essai analysé est de 242,8 µmol/L (v/v).
Compte tenu de la dilution réalisée dans la fiole jaugée, on déduit :
[potassium]_{"échantillon à doser"} = 242,8 * 100/90 # 270 µmol/L .

3.4 Conclusion

On voit l'intérêt de l'étalon interne dans ce dosage :
On ne connait pas l'état de dérive de l'appareillage lors de chaque mesure de signal, mais on est en droit de d'énoncer qu'elles se produisent selon la même proportion pour l'étalon interne et pour l'analyte à mesurer (ça, il faut bien comprendre qu'on le sait par une connaissance du fonctionnement de l'appareil !!). Ainsi, C'est l'étalon interne qui peut nous renseigner à chaque mesure de signal. Et la qualité des mesures est ainsi améliorée (fidélité).

Remarque. Pour qui y regarde de près, l'étalonnage interne pratiqué ici compense aussi les erreurs sur les ajustages des fioles jaugées utilisées dans la gamme. Pas les pipetages, pas pour l'essai comme il est réalisé.

Voyez aussi comment calculer l'exemple ci-dessus de façon plus générale et plus formelle en lisant le paragraphe 4.

3.5 Bibliographie

J.P. Péré, Techniques spectroscopiques en biochimie analytique, CRDP Bordeaux-Aquitaine (1999).