4. Utilisation d'un étalon interne : tentative de généralisation
On va essayer de rassembler tous les éléments d'intérêt des étalons internes
évoqués séparément dans les 3 exemples ci-dessus dans un cas formel de portée "globale".
On doit néanmoins préciser les éléments choisis :
- l'analyse exige un traitement préalable de l'échantillon ;
- la détection met en oeuvre un "volume injecté" non strictement déterminé ;
- le signal récupéré lors de la mesure des analytes est un signal proportionnel
selon un coefficient de réponse caractéristique mais la réponse finale est soumise à
dérives, fluctuations.
Le schéma ci-dessous essaie de résumer la situation :
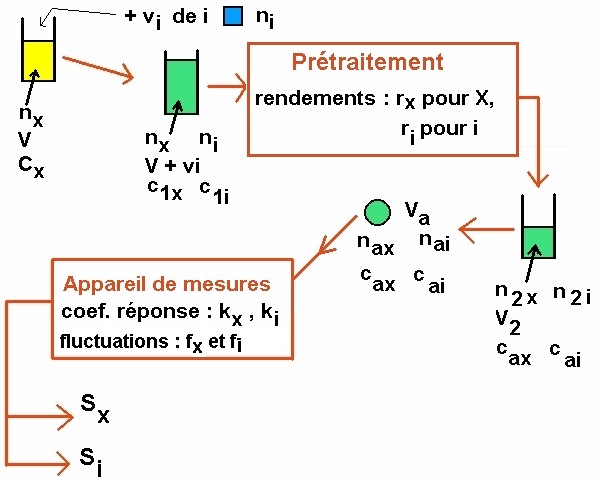
|
Echantillon de volume V, de concentration Cx. Soit n
x la quantité de X :
nx = Cx * V
On ajoute un volume Vi d'étalon interne i
contenant ni moles de i. Les concentrations respectives en X
et en i deviennent alors C1x et C1i.
Le prétraitement conduit à récupérer un volume V2
contenant n2x et n2i moles de X et de i. Les concentrations
respectives en X et en i deviennent alors Cax et Cai.
Si on appelle respectivement rx et ri
les rendements du prétraitement pour X et i ; on a :
n2x = rx * nx
et
n2i = ri * ni
On suppose que l'appareil analyse sur un volume
Va (volume "injecté") et mesure ainsi les quantités nax et nai
qui répondent à :
nax = Cax * Va
et
nai = Cai * Va
On suppose une mesure quantitative avec des signaux
respectifs Sx et Si pour X et i et des facteurs de réponse
kx et ki qui obéissent à :
nax = kx * fx * Sx
et
nai = ki * fi * Si.
où fx et fi représentent le facteur de dérive/fluctuation
du coefficient de réponse à un instant donné sur la mesure de x et i respectivement.
|
|
On va maintenant établir les 2 relations nx = f(Sx) et
ni = f(Si).
On va voir qu'elles font intervenir rx, V2, Va,
kx, fx
et ri, V2, Va, ki,
fi respectivement.
Et ceci nous permettra de démontrer que l'étalon interne joue le rôle "d'espion" :
- c'est lui qui "fournit" les valeurs de V2, Va ;
- et c'est lui qui permet de s'affranchir des variations sur
rx, kx et fx
lors de chaque mesurage à la condition que ri, ki et fi
subissent les mêmes variations relatives pour le même mesurage.
|
"Démonstration". |
Rappel des étapes en cause.
On reprend, par la fin, le schéma du tableau présenté ci-dessus. |
Rappel des égalités vues dans le
tableau ci-dessus. |
|
On a supposé des réponses proportionnelles aux quantités injectées mesurées avec
fluctuations de réponses (6), soit :
nax = kx * fx * Sx
et
nai = ki * fi * Si
Donc en "injectant" les relations données dans (5), on obtient :
Cax * Va = kx * fx * Sx
Cai * Va = ki * fi * Si
|
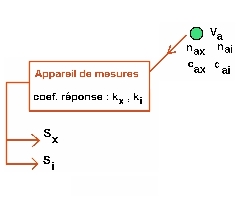
|
(6) On suppose une mesure quantitative avec des sorties
respectives Sx et Si pour X et i et des facteurs de réponse
kx et ki qui obéissent à :
nax = kx * fx * Sx
et
nai = ki * fi * Si.
(5) On suppose que l'appareil analyse sur un volume
Va (volume d'injecté). Il mesure donc les quantités nax et nai
telles que :
nax = Cax * Va
et
nai = Cai * Va |
Or on a Cax = n2x / V2
et
Cai = n2i / V2 (d'après (3))
donc on peut écrire :
(n2x / V2) * Va =
kx * fx * Sx
et
(n2i / V2) * Va =
ki * fi * Si
Utilisons alors les relations liées aux rendements du prétraitement pour X et i données
par (4), on arrive à :
(nx * rx / V2) * Va =
kx * fx * Sx
et
(ni * ri / V2) * Va =
ki * fi * Si
|
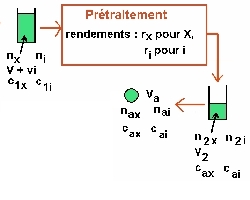
|
(3) Le prétraitement conduit à récupérer un volume V2
contenant n2x et n2i moles de X et de i. Les concentrations
respectives en X et en i deviennent alors Cax et Cai.
(4) Si on appelle respectivement rx et ri
les rendements du prétraitement pour X et i ; on a :
n2x = rx * nx
et
n2i = ri * ni
|
On peut donc écrire - au choix -la relation fondamentale :
(nx / ni) = (ri / rx) *
(kx / ki) * (fx / fi) *
(Sx / Si)
ou
(C1x / C1i) = (ri / rx) *
(kx / ki) * (fx / fi) *
(Sx / Si)
Posons alors quelques remarques :
- le volume "injecté" Va n'apparait plus, il n'a pas à être déterminé pour
chaque mesure ponctuelle. Il est
le même pour l'étalon externe et interne pour chaque mesure ponctuelle
et cela suffit à notre affaire.
- ( kx / ki ) est un rapport constant pour l'analyte X à doser
et l'étalon interne I valable pour une série de mesures.
- La plupart des appareils de mesures permettant de mettre en oeuvre l'étalonnage
avec étalon interne ont un principe de construction qui engendre
fx = fi à tout instant et donc fx / fi = 1
à tout instant .
- Les protocoles d'extraction-préparation des échantillons sont incapables
de permettre de maitriser les valeurs de rx et ri mais il est
assez simple de les concevoir de telle sorte que ri / rx = 1
.
Conclusion :
Grâce à l'étalon interne, à qui il arrive ce qu'il arrive à l'analyte à doser,
on obtient une relation simple qui permet
de "contourner" astucieusement tous les "inconnus" du problème :
(nx / ni) = * ( kx / ki )
(Sx / Si) (relation (F1))
ou
(C1x / C1i) = * ( kx / ki )
(Sx / Si) (relation (F2))
avec ( kx / ki ) coefficient caractéristique parfaitement
constant dans une série de mesures. ( kx / ki )
sera connu très facilement par
la mise en oeuvre d'un étalonnage avec des solutions contenant X et I en quantités connues.
Ainsi se termine le traitement du "cas général".
Mais pour rester concret appliquons le aux 3 cas évoqués précédemment...
|
Application au cas n° 1, le dosage d'adrénaline.
Revoyez éventuellement le cas ...
Les résultats obtenus avec le mélange des 2 étalons adrénaline et DHBA |
Les résultats de Monsieur Dupont |
Les résultats de Madame Durand |
3 pg d'adrénaline et 5 pg de DHBA conduisent à des pics de surfaces respectives
230673 et 557 219 unités. |
Un volume essai E de 1,00 mL de plasma auquel on ajoute 50 µL d'une solution de DHBA
qui apportent ainsi 500 pg de DHBA conduisent à un pic adrénaline de surface
96 620 unités et un pic DHBA de surface 429 766 unités. |
Un volume essai E de 1,00 mL de plasma auquel on ajoute 50 µL d'une solution de DHBA
qui apportent ainsi 500 pg de DHBA conduisent à un pic adrénaline de surface
174532 unités et un pic DHBA de surface 397 562 unités. |
On applique la relation (F1) sans sourciller, presque sans réfléchir au problème,
et on obtient instantanément : |
3 / 5 = (kx / ki) *
(230673 / 557219)
soit
(kx / ki) = (3 / 5) * (557219
/ 230673)
|
nx / 500 = (kx / ki)
* (96620 / 429766)
soit
nx = (kx / ki)
* (96620 / 429766) * 500
|
nx / 500 = (kx / ki)
* (174532 / 397562)
soit
nx = (kx / ki)
* (174532 / 397562) * 500
|
D'où : |
nx = (3 / 5) * (557219
/ 230673)
* (96620 / 429766) * 500
qui donne
nx = 163 pg ; et ce dans 1,00 mL de plasma ...
|
nx = (3 / 5) * (557219
/ 230673) * (174532 / 397562) * 500
qui donne
nx = 318 pg ; et ce dans 1,00 mL de plasma ...
|
Application au cas n° 2, le dosage d'éthanol.
Revoyez le cas à la lumière de l'explication ci-dessous :
La fonction d'étalonnage est une application directe de la relation (F2).
Il n'y a pas, dans ce cas, de traitement préalable des échantillons. L'étalon
interne "espionne" les fluctuations au niveau de l'injection et de la détection.
Application au cas n° 3, dosage de potassium.
Revoyez le cas à la lumière de l'explication ci-dessous :
La fonction d'étalonnage est une application directe de la relation (F2).
Il n'y a pas, dans ce cas, de traitement préalable des échantillons. L'étalon
interne "espionne" les fluctuations au niveau du débit d'injection, de la flamme
et de la détection.


