Chémostat

3. Le chémostat en équilibre dynamique

Ce chapitre est tout à fait accessible à bac2 (à condition d'avoir suivi les cours de maths dédiés aux équations différentielles de ces programmes et de vouloir jouer avec ça dans le cadre d'un chémostat). Donc c'est pour ceux qui aiment combiner un peu maths et biologie ...ou qui ont des insomnies.

On rappelle le système d'équations qui règle le modèle simple de chémostat envisagé (modèle de Monod, voir $2) :

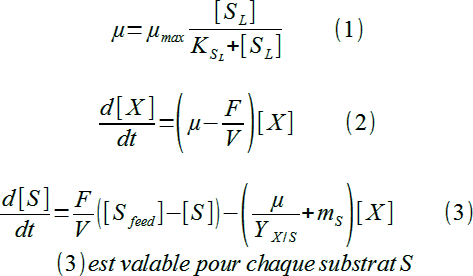
Il n'est pas question ici de travailler ce système d'équations au niveau mathématique, on admettra simplement qu'un tel système va converger vers 2 états stationnaires possibles pour lesquels d[X]/dt = 0 et d[S_l]dt = 0 et qui seront :
• L'état de lavage si F/ V (taux de renouvellement du réacteur) est trop élevé. Ca pousse moins vite que ça ne sort, le réacteur se vide peu à peu de sa biomasse.
• L'état stationnaire dynamique pour lequel on atteint une biomasse constante non nulle dans le réacteur ainsi qu'une constance des concentrations en substrats.

3.1 lavage ou dynamique stationnaire

L'équation (2) est remarquable si on admet que le chémostat entre en état stationnaire dynamique, état pour lequel on aura donc d([X])/dt = 0. L'équation montre (2) qu'on aura d[X]/dt=0 pour (µ - F/ V) = 0 soit µ = F/V. A l'état d'équilibre dynamique d'un chémostat µ = F/ V.

Note : dans beaucoup d'ouvrages de génie fermentaire, F/ V, taux de renouvellement du milieu, est désigné par la lettre D, d'où les classiques formules µ=D.

L'état de lavage est obtenu quand on applique des valeurs de F/ V > µ_max : on dépasse la capacité des micro-organismes à se multiplier face à l'effet de lavage.

3.2 Illustration par un cas pratique

Soit le chémostat suivant :

• V = 10 L, F = 2,5 L.h^-1. Soit D = F/ V = 0,25 h^-1 (soit un temps de séjour moyen de 1/D = 4h dans le fermenteur)
• Alimentation avec un milieu contenant un substrat S_L qui deviendra limitant de la vitesse spécifique de croissance avec [S_L-feed] = 50 g/L
• µ_max souche utilisée = 0,46 h^-1
• K_{S_L} = 1 g/L (pour le substrat S_L)
• Rendement de production de biomasse sur le substrat S : Y_X/S = 0,45 g/g (g de biomasse sèche pour 1 g de S_L consommé)
• Coefficient de maintenance pour le substrat S_L limitant : m_{S_L} = 0,05 g.g^-1.h^-1 (g de S_L par g de biomasse et par heure)

La résolution "théorique" du chémostat à l'état stationnaire est très simple

L'équation (2) pour d[X]/dt=0 (état stationnaire) donne µ = D = 0,25 h^-1

En réinjectant la valeur de µ dans l'équation (1), on obtient :
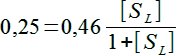chemostat_3_im1 (1K) soit 0,25(1+[S_L])=0,46[S_L]
D'où on tire [S_L] = 1,19 g/L

Il suffit maintenant de tout injecter dans l'équation (3) pour l'état stationnaire où d[S_L)]/dt=0 pour obtenir [X] :
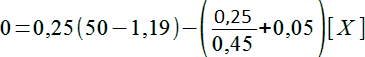
chemostat_3_im2 (3K)
D'où on tire [X] = 20,15 g/L (biomasse sèche)

Cet état stationnaire est indépendant de la valeur de départ de [X] (à l'inoculation du chémostat). On peut modéliser la dynamique des 3 équations du chémostat avec un programme informatique. Ci-dessous voici, en image, la modélisation du chémostat (mêmes paramètres que pour les calculs ci-avant) pour 4 valeurs inoculum différentes, 0,1 g/L ; 1 g/L ; 5 g/L et 15 g/L. On va toujours vers le même équilibre dynamique. :

Que se passerait-il pour F = 6 L.h^-1 ? On a alors D = F/V = 0,6 h^-1 qui est supérieur à µ_max. Le chémostat passe en mode "lavage" (washing-out), la biomasse va peu à peu tendre vers 0.

On peut utiliser la même modélisation informatique des 3 équations du chémostat que ci-avant en réglant D à 0,6 h^-1. La figure ci-dessous montre la convergence vers le lavage.

3.3 Annexe : le script Python utilisé pour les calculs de modélisation

Pour ceux que ça intéresse, voici le script Python utilisé. Avec ODEINT() évidemment. Je suis preneur de critiques...

import numpy as np     #import des bibliothèques de calculs numériques (numpy)
import matplotlib.pyplot as plt     #import des bibliothèques de calculs numériques (numpy) et de tracés matplot), je suis en standard et pas en pylab
from scipy.integrate import odeint     #import de ODE intégration

mumax=0.46     #vitesse spec. max de croissance en h-1
K50s=1     #le K50 pour la source limitante
YXsurS=0.45     #rendement YX/S g de X par g de S pour la croissance
m=0.05     # coef de maintenance g de S par g de X et par h
Sfeed=50     # conc en S dans l'alimentation en g/L
D=0.25     # taux de renouvellement = F/V en h-1 dit être < à mumax pour ne pas aller au lavage

bminit_a=0.1     # les 4 valeurs de [X] à t=0
bminit_b=1
bminit_c=5
bminit_d=15

duree=35     #durée de culture en h

    #dans le système d'équadif ci-dessous, y[0] sera la biomasse et y[1] sera le substrat
def eqdif(y, t):     #second membre de l'equa diff (y') ATTENTION on met le y d'abord avant le t y(t) ....
    return [(mumax*y[1]*y[0]/(K50s+y[1]))-D*y[0], D*Sfeed-D*y[1]-((mumax*y[1]*y[0])/(YXsurS*(K50s+y[1])))-m*y[0]]

t = np.linspace(0, duree, 1000)     #linspace définit l'étendue du tracé (ici de t=0 à duree,) et le nbre de pts (ici 1000 points)
y0=[bminit_a,Sfeed]
y_a = odeint(eqdif, y0, t)     # solution (eqdif comme défini ci-avant, puis on renseigne y0 et t et faut avoir renseigné t avec np.linspace avant !!!)
sols_a = y_a[:,1]
solbm_a=y_a[:,0]

t = np.linspace(0, duree, 1000)     #linspace définit l'étendue du tracé (ici de t=0 à duree,) et le nbre de pts (ici 1000 points)
y0=[bminit_b,Sfeed]
y_b = odeint(eqdif, y0, t)     # solution (eqdif comme défini ci-avant, puis on renseigne y0 et t et faut avoir renseigné t avec np.linspace avant !!!)
sols_b = y_b[:,1]
solbm_b=y_b[:,0]

t = np.linspace(0,duree, 1000)     #linspace définit l'étendue du tracé (ici de t=0 à duree,) et le nbre de pts (ci-dessous 1000 points)
y0=[bminit_c,Sfeed]
y_c = odeint(eqdif, y0, t)     # solution (eqdif comme défini ci-avant, puis on renseigne y0 et t et faut avoir renseigné t avec np.linspace avant !!!)
sols_c = y_c[:,1]
solbm_c=y_c[:,0]

t = np.linspace(0, duree, 1000)     #linspace définit ... etc ... voir ci-dessus ...
y0=[bminit_d,Sfeed]
y_d = odeint(eqdif, y0, t)     # solution (eqdif comme défini ci-avant, puis on renseigne y0 et t et faut avoir renseigné t avec np.linspace avant !!!)
sols_d = y_d[:,1]
solbm_d=y_d[:,0]

fig, ax1=plt.subplots()     #ax1 représente la figure hôte
axy2 = ax1.twinx()     #axy2 emmène l'axe 2 des y
p1_a, = ax1.plot(t, solbm_a, 'r', label='[X]t0 exp. a')
p1_b, = ax1.plot(t, solbm_b, 'r--', label='exp. b')
p1_c, = ax1.plot(t, solbm_c, 'r:', label='exp. c')
p1_d, = ax1.plot(t, solbm_d, 'r-.', label='exp. d')
p2_a, = axy2.plot(t, sols_a,'b', label='[S] exp. a')
p2_a, = axy2.plot(t, sols_b,'b--', label='exp. b')
p2_a, = axy2.plot(t, sols_c,'b:', label='exp. c')
p2_a, = axy2.plot(t, sols_d,'b-.', label='exp. d')

ax1.legend(loc=1, borderaxespad=1.)     # à placer après le plot pour faire apparaître son label
axy2.legend(loc=4, borderaxespad=1.)
plt.xlim(0,duree+15)
    #plt.ylim(0,1.5) # à "dés #" pour zoomer l'équilibration du substrat

ax1.set_xlabel('Temps h')
ax1.set_ylabel('[biomasse] g/L', color='r')
axy2.set_ylabel('[S] g/L', color='b')
plt.title("Modélisations d'un chémostat, modèle de Monod")
plt.show()     # affiche la figure a l'ecran

retour en haut de page