3. Estimateur non biaisé de l'écart-type
La loi normale parente est de moyenne µ et d'écart-type σ. Soit V(X) sa variance, V(X)=σ2
On suppose qu'on tire des échantillons d'effectif n au sein de cette loi normale parente.
• Comme on l'a vu dans le paragraphe précédent (s)2=Σ(xi-m)2/(n-1) est un estimateur sans biais de V(X)=(σ)2 (ce qui signifie que l'espérance de (s)2 est égale à (σ)2 : E((s)2)=(σ)2)
• En revanche l'écart-type expérimental s=racinecarré[Σ(xi-m)2/(n-1)] est un estimateur biaisé de σ.
Cela peut paraître surprenant mais l'espérance de s n'est pas égale à σ ! Ainsi qui souhaite avoir un estimateur non biaisé de σ à partir de s devrait appliquer un facteur correctif. Le tableau ci-dessous donne des valeurs de facteurs correctifs pour différentes valeurs de n. Plus n est grand plus le facteur correctif tend vers 1.
n | Il faut multiplier s par d |
|
d | d | |
2 | non calculé | 1,238 |
3 | non calculé | 1,125 |
4 | 1,085 | 1,084 |
5 | 1,064 | 1,065 |
6 | 1,051 | 1,047 |
7 | 1,042 | 1,046 |
8 | 1,035 | 1,034 |
9 | 1,032 | 1,030 |
10 | 1,028 | 1,026 |
12 | 1,023 | 1,017 |
15 | 1,018 | 1,014 |
20 | 1,013 | 1,007 |
30 | 1,009 | non donné |
(*) Sur le site du NIST (engineering statistics, e-Handbook of Statistical Methods,
http://www.itl.nist.gov/div898/handbook/) et en
particulier la page http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc32.htm. L'article donne la relation s=c4σ avec
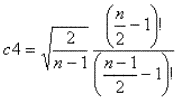(donc dans le tableau d=1/c4)
Remarque : (n/2)! avec un entier n impair se calcule selon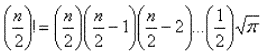 
(**) D'après un article de J-M POU, "Ecart-type expérimental, quelle formule choisir ?", article disponible à http://www.deltamuconseil.fr/download/Presse/Conference-poster.pdf
Pour ceux qui aiment les justifications, voilà quelques explications à cette histoire de biais sur l'écart-type expérimental et de facteur correctif. Tout vient du fait que la racine carré d'une moyenne de variances expérimentales non biaisées n'est pas égale à la moyenne des racines carrés des variances expérimentales ...
Imaginez que vous ayez à disposition p=10000 échantillons d'effectif n de la loi normale parente. Chacune des variances expérimentales obtenue serait un estimateur non biaisé de la variance vraie. Et donc une très bonne estimation non biaisée de σ serait la racine carré de la moyenne des variances (la racine carré de la somme de toutes les variances divisée par leur effectif = racine carré de [Σ((s)2)/p]). Si vous faites la moyenne des écart-types expérimentaux, vous allez faire la somme des racines carré de toutes les variances expérimentales s obtenues puis vous allez diviser par l'effectif = Σs/p. Or racine carré de [Σ((s)2)/p] est supérieur à Σs/p. Là est l'origine du biais sur s. Vous pouvez tester sur une feuille de simulation numérique, en voici une avec le tableur openoffice : exemple de feuille de simulation numérique.
Et voici encore un truc, truc utilisé dans les cartes de contrôle de Shewhart de type R.
• La moyenne de l'étendue des échantillons d'effectif n (l'étendue d'un échantillon c'est la différence entre la valeur max et la valeur min) permet d'obtenir un estimateur de l'écart-type (la relation statistique entre la moyenne de l'étendue pour une distribution normale et σ a été tabulée par Patnaik en 1946). Voici une table de valeurs de facteurs d2. L'estimation de σ est obtenue en divisant l'étendue par d2. Jusqu'à n=5 la moyenne des étendues des échantillons d'effectif n donne un estimateur simple à établir de σ et assez efficace. Au delà vaut mieux calculer l'écart-type expérimental.Effectif n des échantilons | d2 |
2 | 1,128 |
3 | 1,693 |
4 | 2,059 |
5 | 2,326 |
6 | 2,54 |
7 | 2,71 |
8 | 2,84 |
9 | 2,97 |
10 | 3,08 |