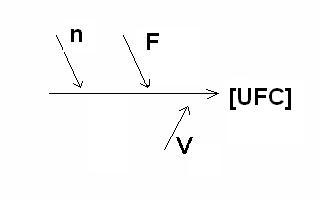
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque n, F et V sont des variables indépendantes.
Retour accueil | Droit de copies | Sommaire de ce dossier | Page Précédente | Page Suivante
Comment évaluer les incertitudes des numératons bactériennes par les méthodes dénombrant des unités formant colonie (UFC). Etude d'un exemple simple.
1. Description du mesurage et relation fondamentale du mesurage
On suppose un échantillon liquide (eau, urine ...). Des dilutions en série de raison géométrique 1/10 sont réalisées (1 mL + 9 mL de diluant). Deux boîtes de culture sont ensemencées par dilution sous un volume de 1 mL. Après incubation, on compte les unités formant colonies.
Données concernant les dilutions réalisées et les inoculum :
Données concernant les résultats obtenus :
nombre de boites comptées | UFC comptées |
volume inoculum "équivalent" vi |
dilution 10-3 |
40 |
1 mL |
49 |
1 mL | |
dilution 10-4 | 3 |
0,1 mL de dilution 10-3 |
7 |
0,1 mL de dilution 10-3 | |
somme = n = 99 |
somme = V = 2,2 mL de dilution 10-3 (F, facteur de dilution inverse = 103 sans correction de biais = 9,963 après correction) |
Formule du mesurage :
Application numérique :
2. Identification et analyse des sources d'imperfection dans le processus de mesure
C'est la formule du mesurage qui va nous donner le départ pour le recensement
des sources d'imperfection
(qui peuvent apriori jouer à la fois au niveau d'erreurs systématiques (biais à corriger)
et au niveau de l'incertitude). A savoir :
n, F et V

|
Et ainsi on va commencer le travail en examinant chaque facteur d'influence de près en alliant
imagination et une bonne connaissance du processus de mesure ...
>Il va falloir associer une incertitude-type et éventuellement un facteur de correction
à chaque facteur d'influence, puis combiner
correctement ces incertitudes-types pour calculer l'incertitude-type globale. La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque n, F et V sont des variables indépendantes. |
Déterminer l'incertitude-type sur le volume V ne pose pas trop de problèmes. C'est par là qu'on va commencer. Il suffit de se rappeler que V provient de 4 volumes prélevés : deux prélèvement de 1 mL de dilution 10-3 et deux prélèvements de 1 mL de dilution au 1/10 de cette dilution précédente. Selon ce qui a été écrit dans le paragraphe de description du mesurage appelont "ai" les volume de 1 mL d'inoculation et nécessaires aux dilutions au 1/10 et "bi" les volumes de 9 mL nécessaires pour réaliser les dilutions au 1/10. On peut écrire : V = a1 + a2 + (a3 + a4)/ f
Avec facteur f = (a5+ b)/a5
Avec la remarque fondamentale suivante : les différentes variables ai et bsont indépendantes.
|
a1 = 1 mL |
a3 = 1 mL et ua3 = ua = 0,01 mL |
|||||
|
|||||||
|
Donne après calcul |
||||||
On peut donc calculer uV en appliquant la loi de propagation des écart-types dans ce cas simple de variables indépendantes. On obtient :
0,012 |
0,012 | ||||||
0,0001 |
0,0001 | ||||||
On va maintenant se préoccuper du facteur de dilution 10-3 : F = 9,963. Ce qui sera simple.
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page justifiant la formule qui va être posée ci-dessous pour uF. Consultez éventuellement puis refermez.
uF2 = F2k (uf2 / f2)
Avec k = 3 (on compte à partir de la troisième dilution de la série de raison 1/10)
Avec f = 9,96 (série de dilutions de raison a priori d=1/10, f=10. f=9,96 après correction de biais)
Avec uf2 = 0,0481 (cf. ce qu'on a vu avant pour les dilutions au 1/10 pratiquées).
D'où uF2 = 9,96323(0,0481 / 9,962) = 1420
D'où uF = 37,7 # 38
Et regardons maintenant le paramètre "nombre de colonies comptées" (n).
Là, les affaires paraissent moins simples ... et on peut envisager plusieurs
problèmes :
- q1 La question de l'aléa fondamental de type "loi de Poisson" sur n ;
- q2 La question du discernement des colonies plus ou moins différent selon les opérateurs : facteur t, t à déterminer, ut à déterminer ;
- q3 La question du "rendement" du milieu à permettre des développements à l'identique de colonies : facteur y, y=1, ys à déterminer ;
- q4 La question des variations en UFC liés au stockage de l'échantillon : facteur s, s=1, us à déterminer ;
- q5 La question d'une hétérogénéité de matrice au départ sur le type d'échantillon : facteur m, m=1, um à déterminer ;
Pour ne rien oublier, inscrivons
toutes ces nouvelles problématiques
dans le "diagramme initial des causes et des effets". On est ainsi conduit à
un nouveau diagramme des "causes et des effets" associé à "une nouvelle formule du mesurage".
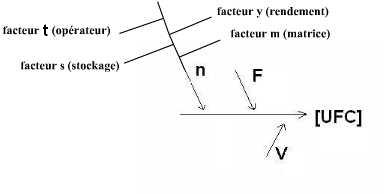
Formule du mesurage : |
Et ainsi on va continuer le travail en étudiant chaque "nouvelle" source
d'imperfection de près ...
Il va falloir associer une incertitude-type et éventuellement une valeur
à chaque source, puis combiner
correctement ces incertitudes-types pour calculer l'incertitude-type globale.
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque toutes les variables sont indépendantes. |
Dans un premier temps de l'étude, on va supposer que les fateurs t, y, s, et m sont à 1 avec une incertitude-type à 0. On envisage uniquement l'aléa sur n. Et la question n'est pas si simple, elle demande une présentation dédiée. Celle si est disponible en activant le lien ici présent qui ouvre une nouvelle page de votre navigateur sur "loi de Poisson et dénombrements d'UFC".
On va utiliser en parallèle les 2 méthodes possibles.
n = 99 UFC est obtenu d'une distribution de Poisson. Et comme dans la loi de
Poisson la moyenne et la variance sont les mêmes, on peut dire que 99 est une estimation de la variance de cette
distribution de Poisson. Ce qui donne un écart-type estimé vers √99 = 9,9. |
Cette méthode nous donne l'incertitude-type sur l'ensemble n/V. Tout se passe comme si une nouvelle variable c=n/V était créée. Il s'agit alors d'obtenir un/V |
On rappelle la formule du mesurage : [UFC] = n F /V u[UFC]2 = (nF/V)2 * (un2/n2
+ uF2/F2 + uV2/V2) On a établi : |
On rappelle la "nouvelle" formule du mesurage : u[UFC]2 =
(c F)2 * (uc2/c2
+ uF2/F2) On peut montrer que : et on a montré que : |
[UFC] = 99 * 9,963 / 2,2 = 44,46 103 UFC/mL u[UFC]2 = ([UFC])2 * (9,92/992
+ 382/9,9632 + 0,0152/2,22)
|
[UFC] = 99 * 9,963 / 2,2 = 44,5 103 UFC/mL u[UFC]2 = ([UFC])2 * (4,52/452
+ 382/9,9632)
|
On a donc estimé l'incertitude-type sur le résultat. Il s'agit maintenant de donner un intervalle de confiance pour le résultat, par exemple un intervalle 95%. La question n'est pas simple puiqu'on va avoir à faire à un dissymétrie.
Activez ce lien pour poursuivre ...
Page mise à jour 10-01-2006 -- JF Perrin -- | Retour accueil | Droits de copies | Sommaire de ce dossier | Page Précédente | Page Suivante
Date de consultation : 12-03-2026