Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2012
[A propos de l'auteur]
[Droits de copie]
Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2012
[A propos de l'auteur]
[Droits de copie]
Le schéma réactionnel du mécanisme bi-bi ordonné à complexe ternaire est le suivant :
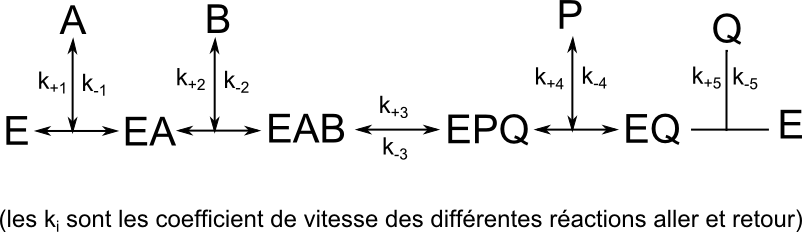
Dans les conditions [A]>>[E0], [B]>>[E0], début de réaction [P] et [Q] suffisamment faibles pour pouvoir négliger les associations retours, il va apparaître un état quasi stationnaire
dont la résolution (pas simple) donne une équation du type :
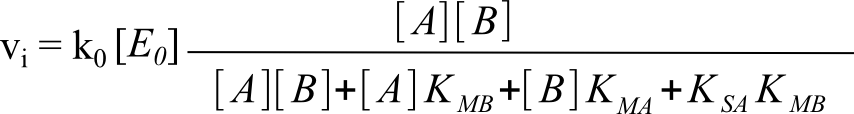
• où KMA = f(ki) est un coefficient appelé coefficient de Michaelis pour A à B saturant et
KMB = f(ki) est un coefficient appelé coefficient de Michaelis pour B à A saturant ;
• où k0 = f(ki) est un coefficient appelé coefficient catalytique de l'enzyme et k0[E0] est la vitesse initiale maximale (asymptotique) à
A et B saturants ;
• où KSA = k-1/k+1 est la constante d'affinité (exprimée en constante de dissociation) de A pour l'enzyme E libre.
Si on divise le numérateur et le dénominateur par [B] dans la formule ci-dessus, on obtient :
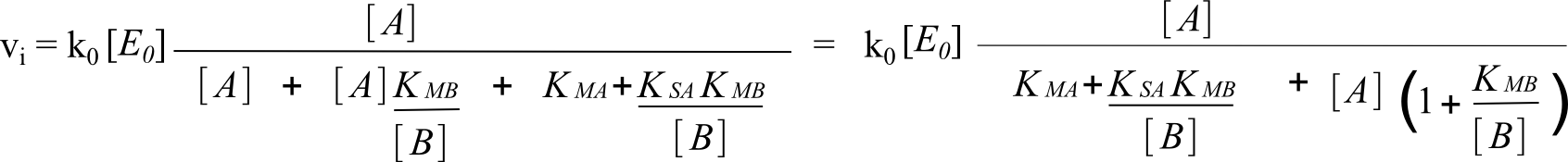
Si on divise le numérateur et le dénominateur par (1+ KMB/[B]) dans la formule ci-dessus, on obtient :
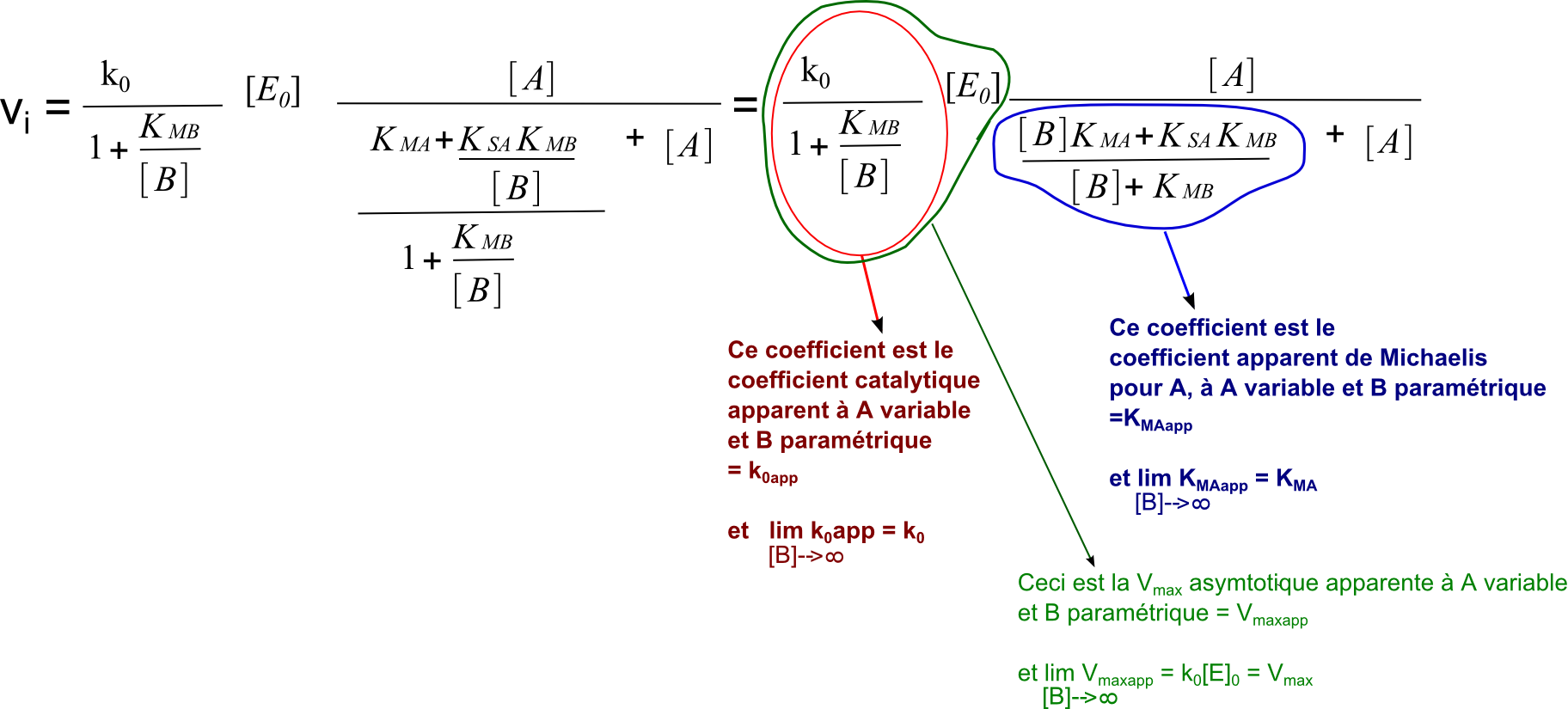
On voit bien que la forme est devenue semblable à la forme classique de présentation de l'équation de Michaelis. Et on voit bien les limites des paramètres lorsque [B] tend vers l'infini, autrement dit lorsque [B] est saturant. En particulier le KMapp qui tend vers KMA. D'où l'appellation pour KMA : coefficient de Michaelis pour A à B saturant.
On travaille l'équation de base selon la même méthode en inversant les rôles de A et B. On obtient :
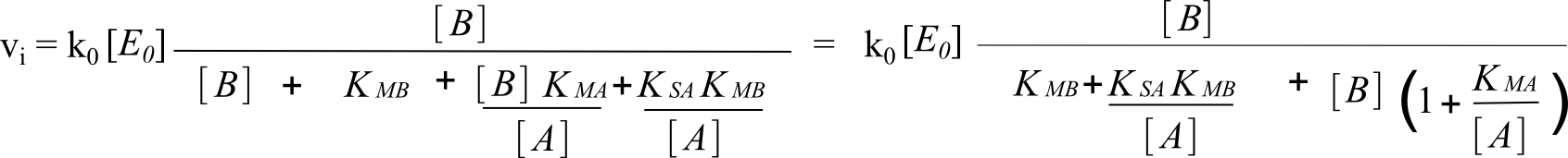
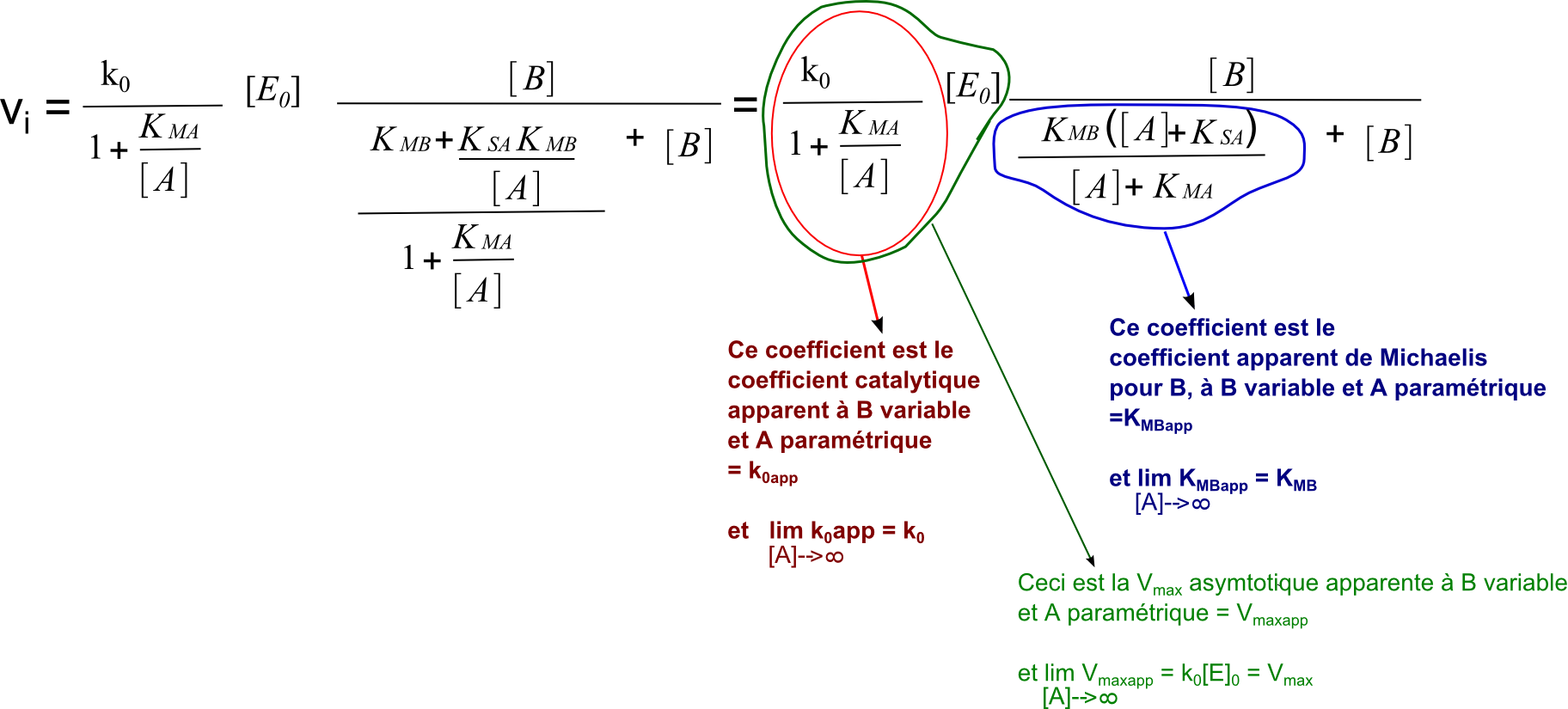
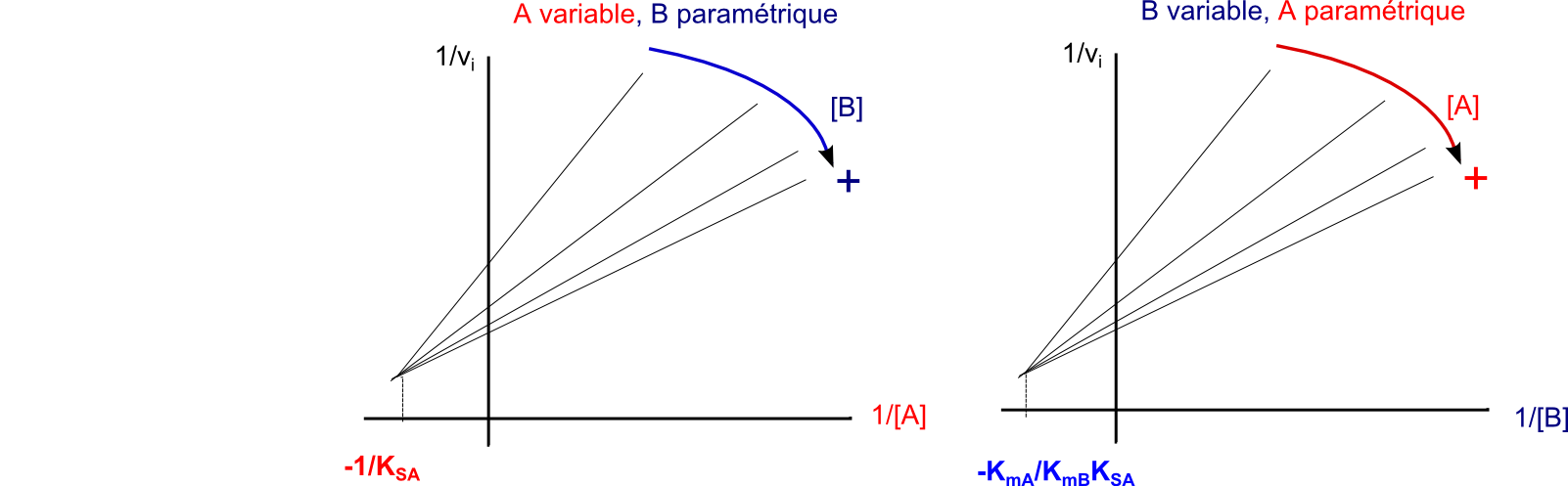
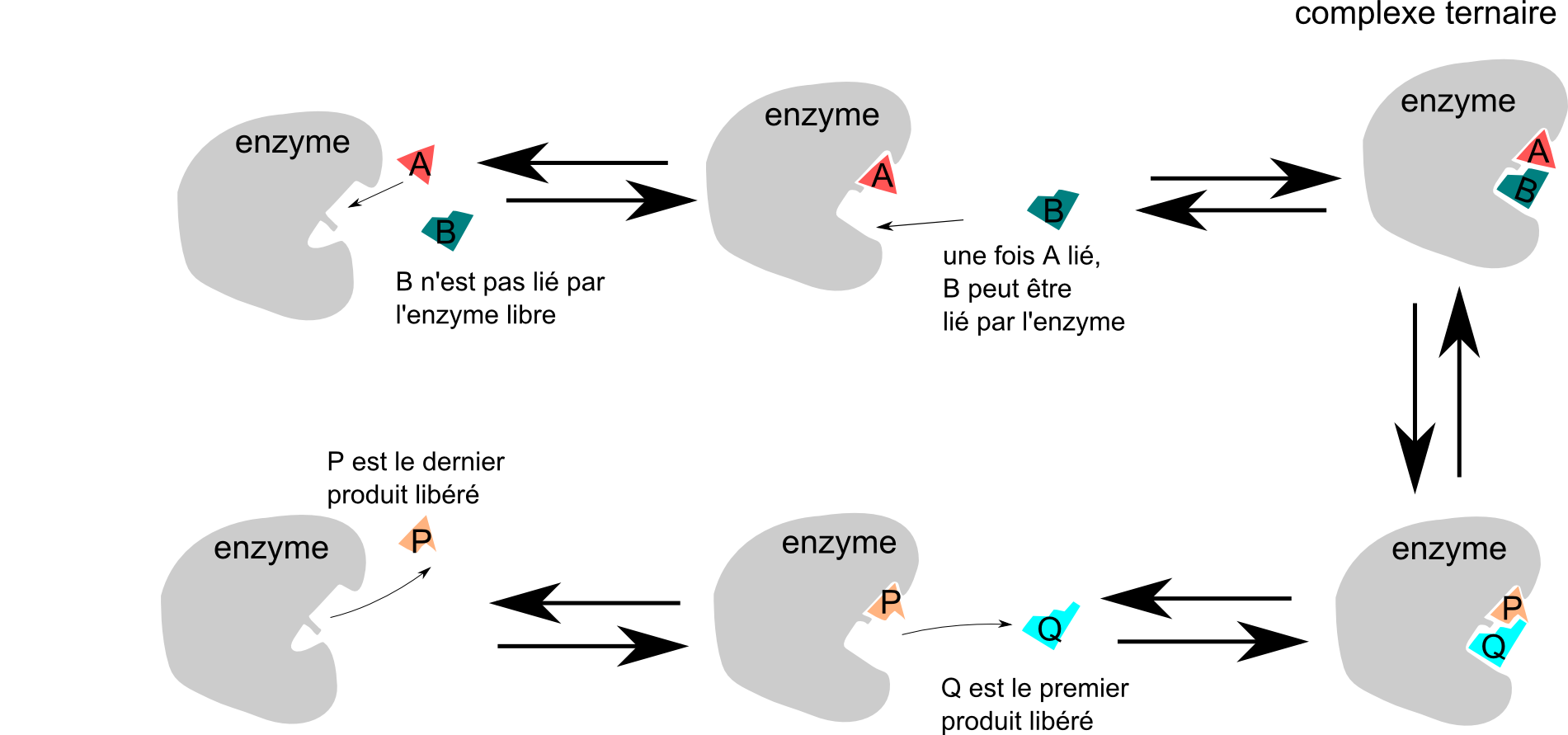
Et un petit schéma qui se veut plus biologique pour illustrer la mécanique ordonnée à complexe ternaire
