Mécanisme bi-bi aléatoire à complexe ternaire et comportement Michaélien

Le schéma réactionnel du mécanisme bi-bi aléatoire à complexe ternaire est le suivant :

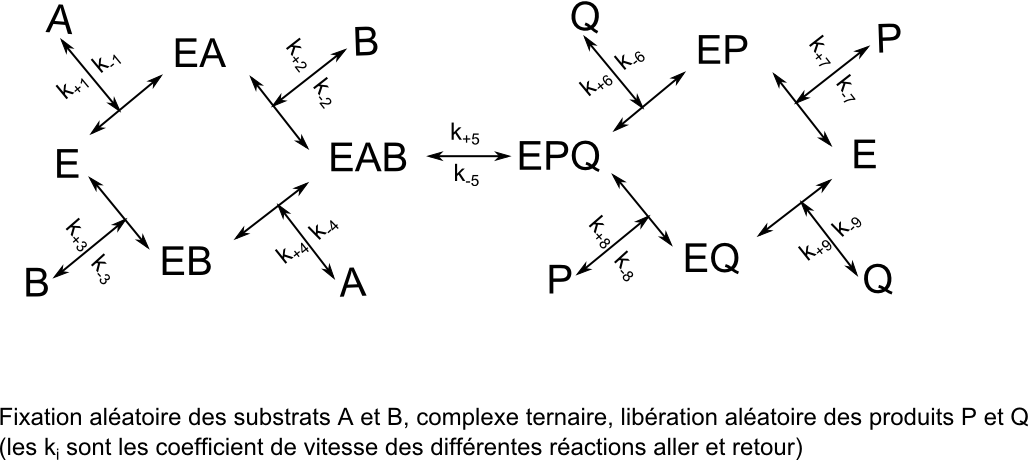
pluriplurimichaelis_bibialeatoire_coef (66K)

Dans ce schéma général, les coefficients d'associations de E avec A ou de EB avec A ne sont pas forcément les mêmes. Il en est ainsi pour les liaisons de B avec E ou EA.

Cette mécanique ne conduit pas forcément à des allures michaéliennes mais y conduit très souvent. On ne retiendra ici ques ces cas. En particulier, dans les conditions [A]>>[E0], [B]>>[E0], début de réaction [P] et [Q] suffisamment faibles pour pouvoir négliger les associations retours et quand les cinétiques d'association/dissociation de E avec A et de E avec B sont très rapides et conduisent au quasi-équilibre, il va apparaître un état quasi stationnaire dont la résolution (pas simple) donne une équation du type :
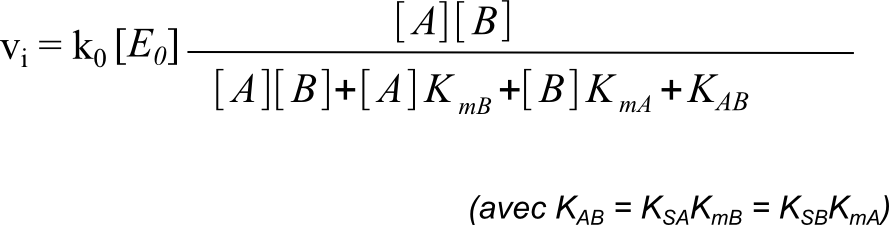
pluriplurimichaelis_bibialeatoire_eq (20K)

• où KmA = f(ki) est un coefficient appelé coefficient de Michaelis pour A à B saturant et KmB = f(ki) est un coefficient appelé coefficient de Michaelis pour B à A saturant ;
• où k0 = f(ki) est un coefficient appelé coefficient catalytique de l'enzyme et k0[E0] est la vitesse initiale maximale (asymptotique) à A et B saturants ;
• où KSA = k-1/k+1 est la constante d'affinité (exprimée en constante de dissociation) de A pour l'enzyme E libre. Et où KSB = k-3/k+3 est la constante d'affinité (exprimée en constante de dissociation) de B pour l'enzyme E libre.

Il est assez simple de montrer alors l'allure michaélienne à A variable et B paramétrique

Si on divise le numérateur et le dénominateur par [B] dans la formule ci-dessus, on obtient :

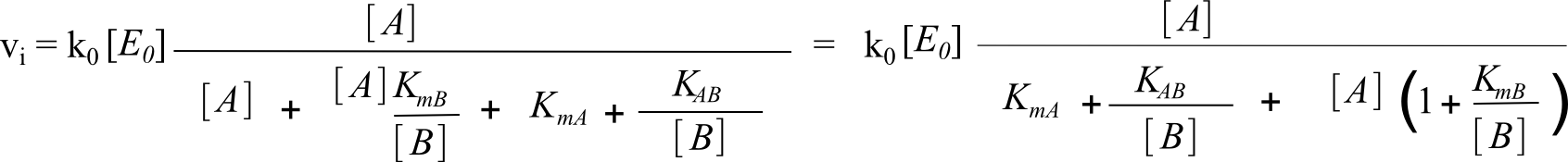
pluriplurimichaelis_bibialeatoire_eq2 (13K)

Si on divise le numérateur et le dénominateur par (1+ KmB/[B]) dans la formule ci-dessus, on obtient :

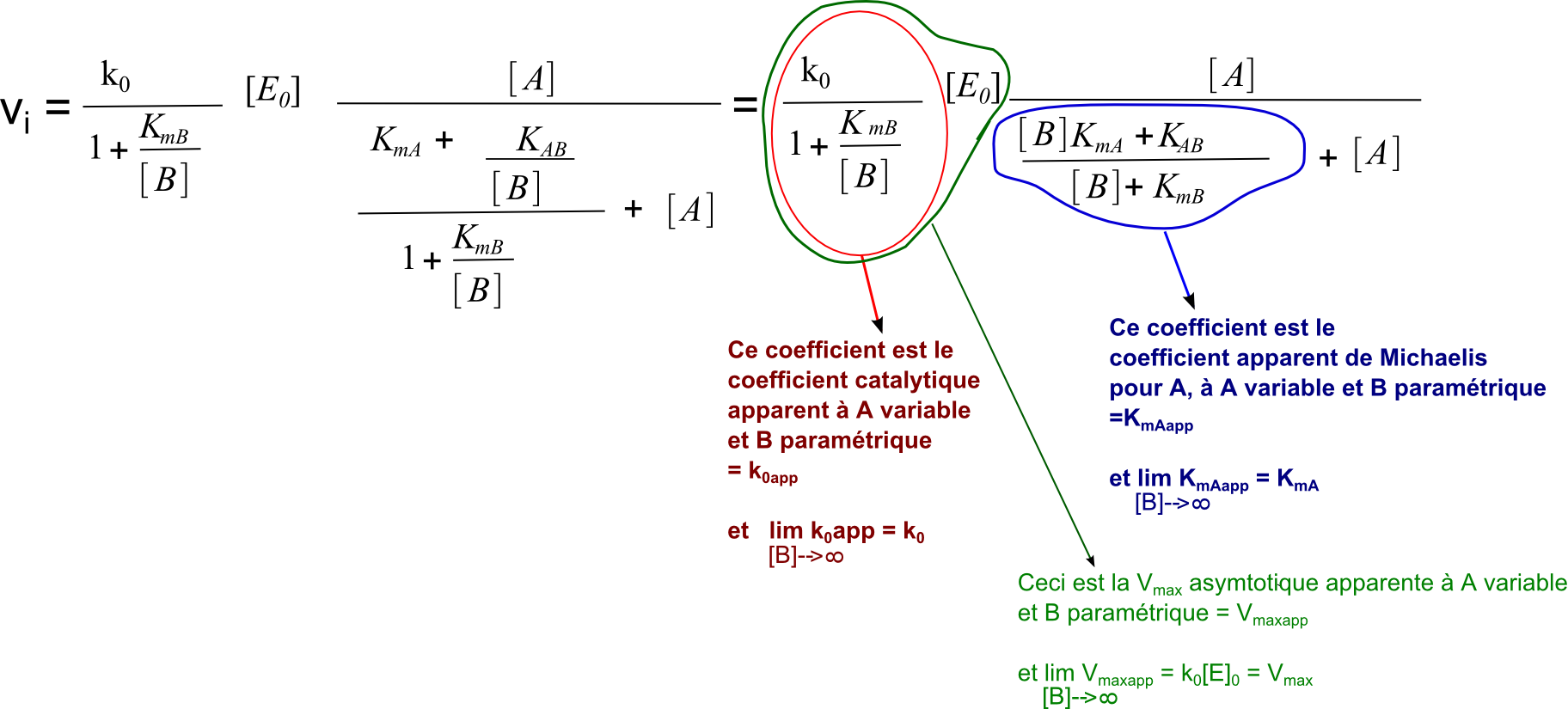
pluriplurimichaelis_bibialeatoire_eq3 (138K)

On voit bien que la forme est devenue semblable à la forme classique de présentation de l'équation de Michaelis. Et on voit bien les limites des paramètres lorsque [B] tend vers l'infini, autrement dit lorsque [B] est saturant. En particulier le Kmapp qui tend vers KmA. D'où l'appellation pour KmA : coefficient de Michaelis pour A à B saturant.

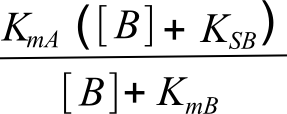Remarque : on a KAB = KmAKSB. A l'aide de cette égalité, on peut réécrire le KmAapparrent comme pluriplurimichaelis_ordonneternaire_eq6 (7K). Cette écriture est plus classique car plus utile lors des tracés en double inverse. On verra ça plus loin.

Il est alors évident de montrer l'allure michaélienne à B variable et A paramétrique puisque A et B jouent des "rôles symétriques"

On travaille l'équation de base selon la même méthode en inversant les rôles de A et B. On obtiendra :

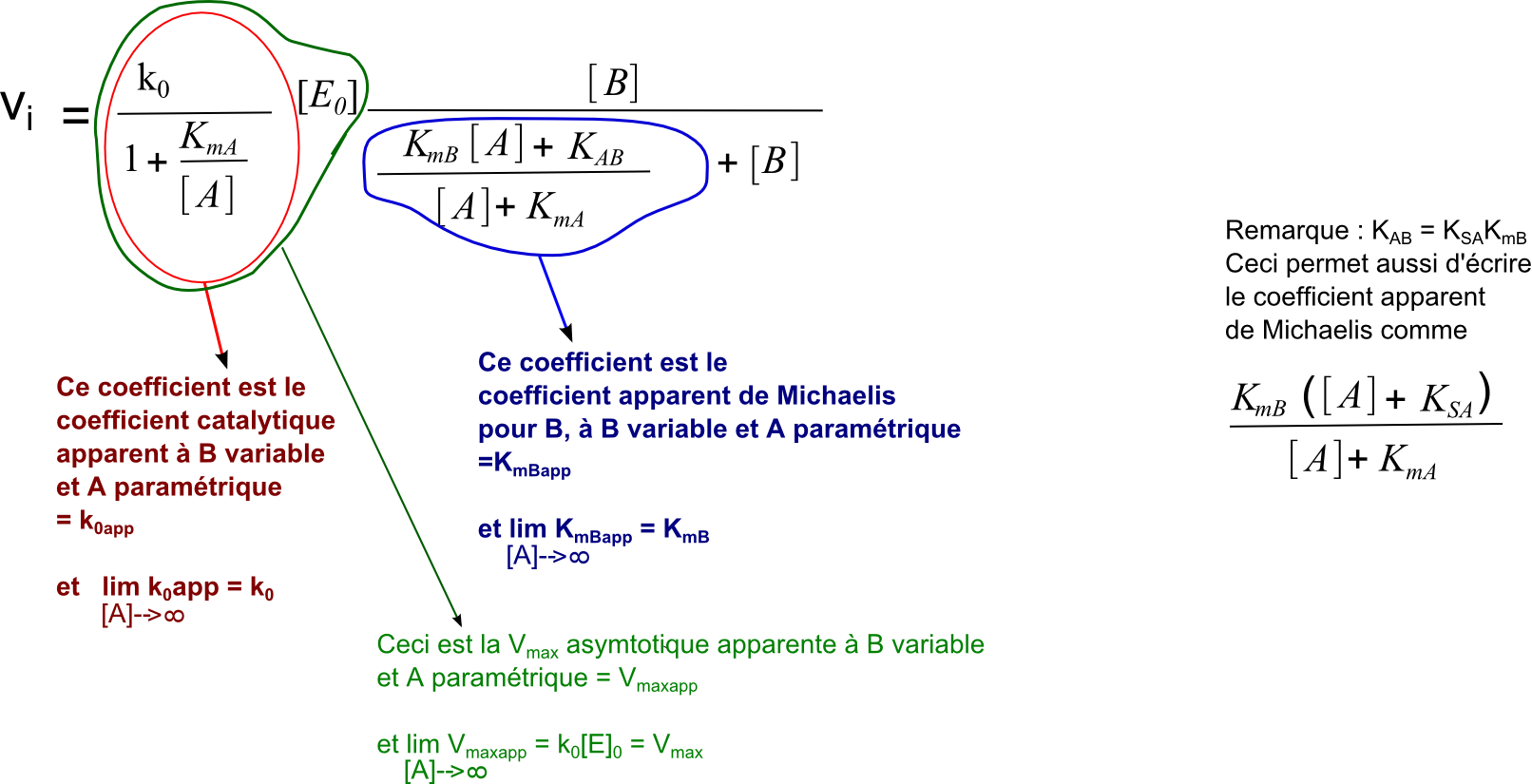
pluriplurimichaelis_bibialeatoire_eq5 (148K)

Les représentations linéarisées en double inverse sont remarquables mais d'allure identique à celles obtenues selon le mécanisme bi bi ordoné à complexe ternaire

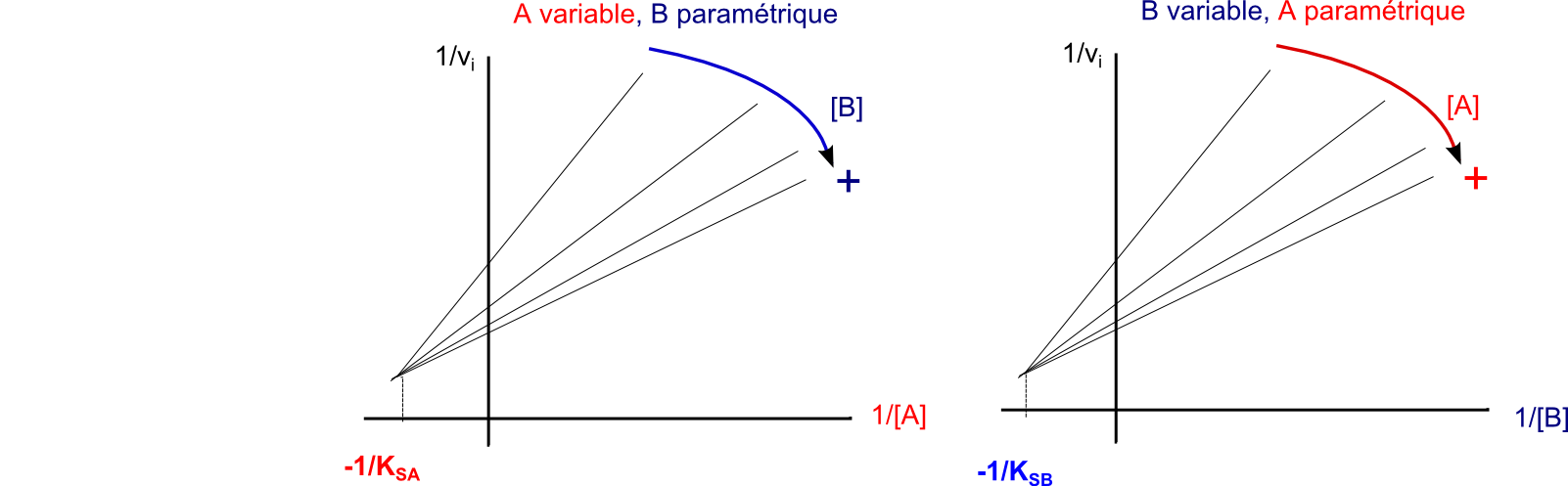
pluriplurimichaelis_bibialeatoire_inverses (57K)

Il n'est pas étonnant que les représentations linéarisées en double inverse soient d'allure identique à celles obtenues selon le mécanisme bi bi ordoné à complexe ternaire puisqu'un mécanisme ordonné n'est en fait qu'un cas particulier de mécanisme aléatoire : celui où un des 2 chemins tend vers une probabilité nulle ... A méditer.

 

Un cas très particulier de mécanisme bi bi aléatoire est finalement assez fréquent : celui où les coefficients de liaisons de A sur E ou EB sont identiques de même que les les coefficients de liaisons de B sur E ou EA. Si en plus, l'acte catalytique est lent devant les équilibres d'association/dissociation de E/EA/EB/EAB, on a :

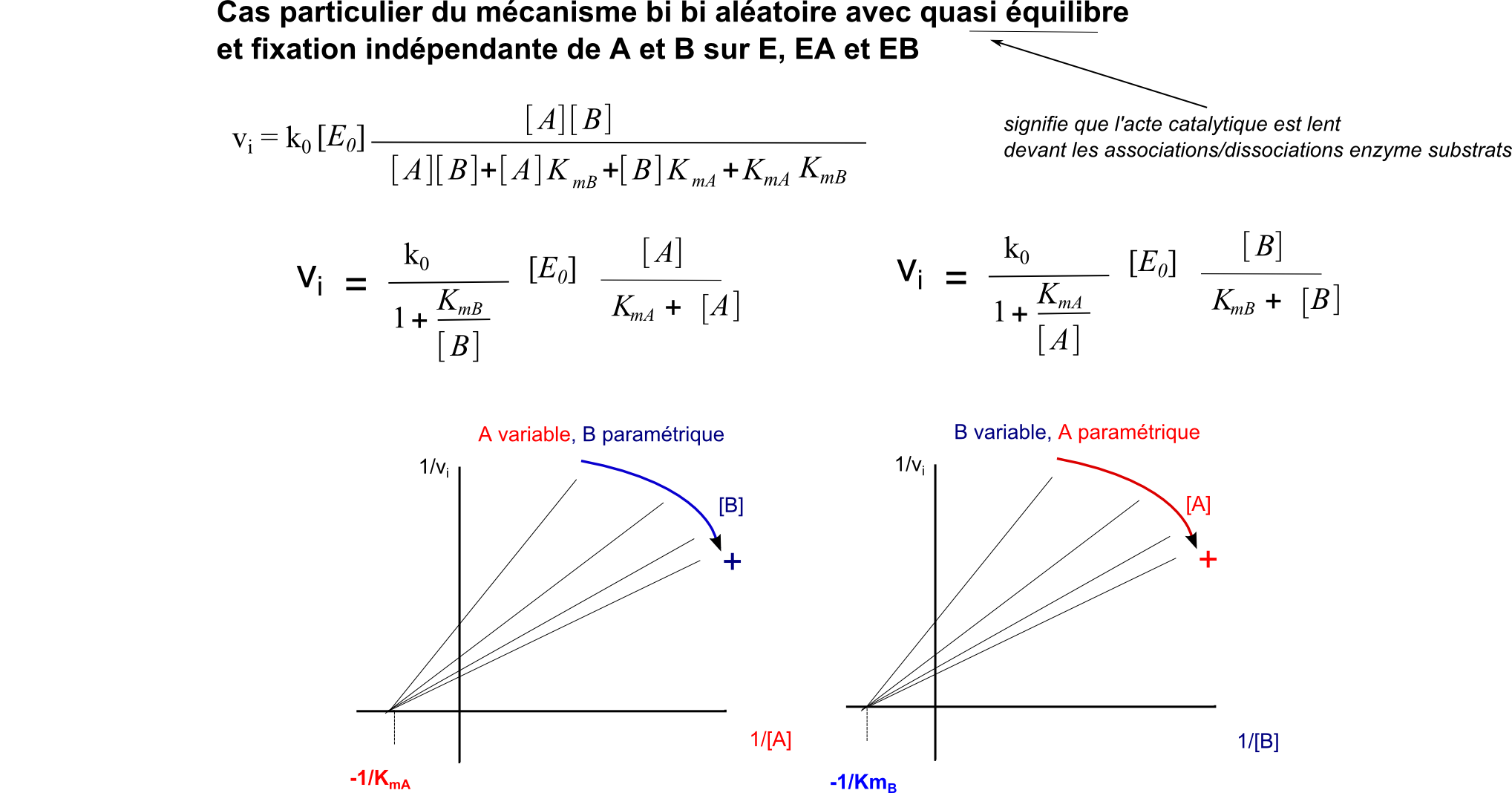
pluriplurimichaelis_bibialeatoireindep_inverses (137K)

Et un petit schéma qui se veut plus biologique pour illustrer la mécanique bi bi aléatoire à complexe ternaire

pluriplurimichaelis_bibialeatoire-espace (185K)