Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2012
[A propos de l'auteur]
[Droits de copie]
Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2012
[A propos de l'auteur]
[Droits de copie]
Le schéma réactionnel du mécanisme bi-bi ping-pong est le suivant :
Dans les conditions [A]>>[E0], [B]>>[E0], début de réaction, il va apparaître un état quasi stationnaire
dont la résolution (pas simple) donne une équation du type :
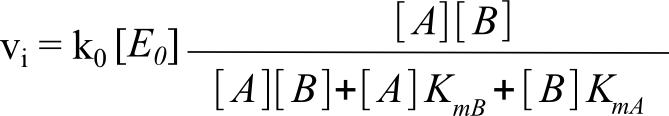
• où KmA = f(ki) est un coefficient appelé coefficient de Michaelis pour A à B saturant et
KmB = f(ki) est un coefficient appelé coefficient de Michaelis pour B à A saturant ;
• où k0 = f(ki) est un coefficient appelé coefficient catalytique de l'enzyme et k0[E0] est la vitesse initiale maximale (asymptotique) à
A et B saturants.
Si on divise le numérateur et le dénominateur par [B] dans la formule ci-dessus, on obtient :
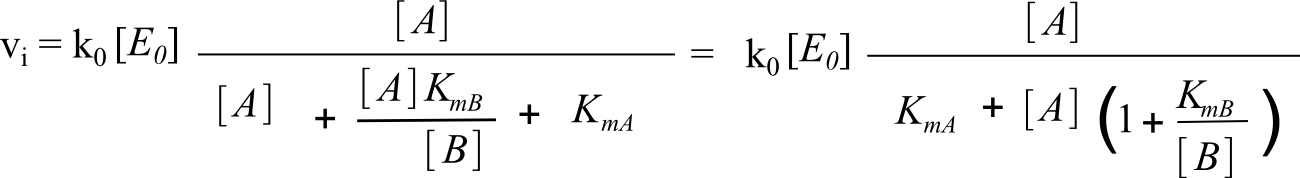
Si on divise le numérateur et le dénominateur par (1+ KmB/[B]) dans la formule ci-dessus, on obtient :
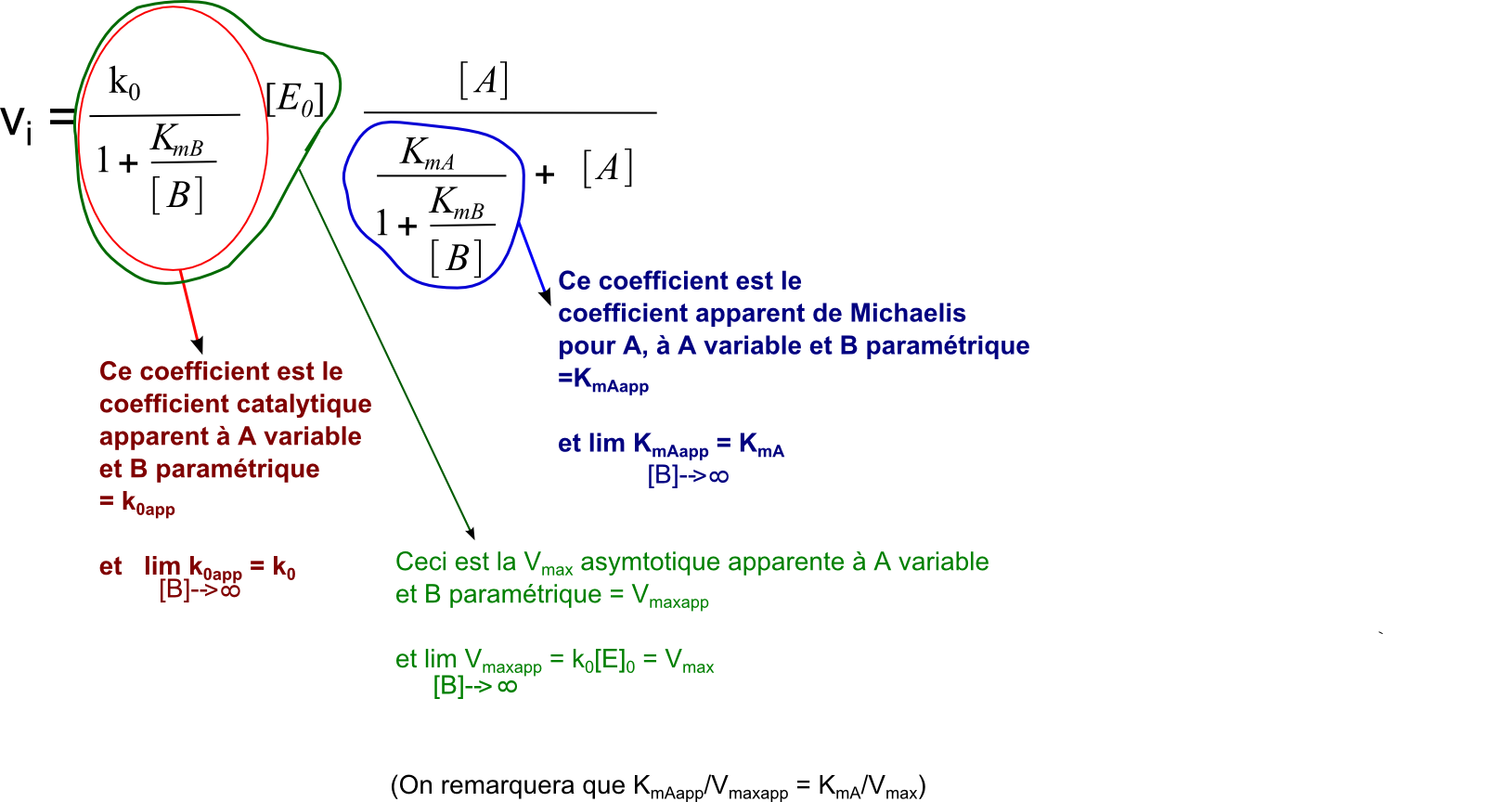
On voit bien que la forme est devenue semblable à la forme classique de présentation de l'équation de Michaelis. Et on voit bien les limites des paramètres lorsque [B] tend vers l'infini, autrement dit lorsque [B] est saturant. En particulier le Kmapp qui tend vers KmA. D'où l'appellation pour KmA : coefficient de Michaelis pour A à B saturant.
On travaille l'équation de base selon la même méthode que ci-dessus. On obtiendra :
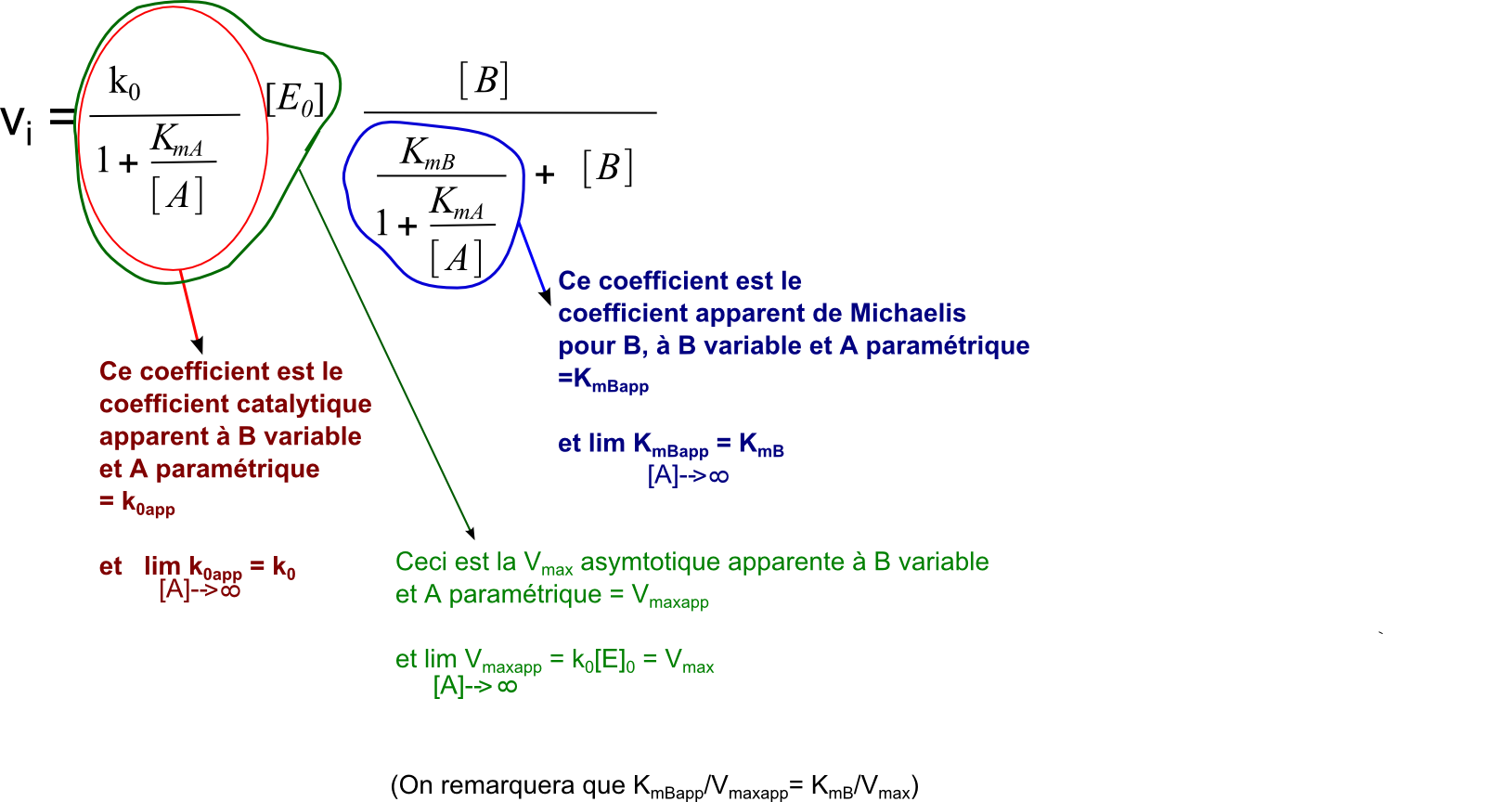
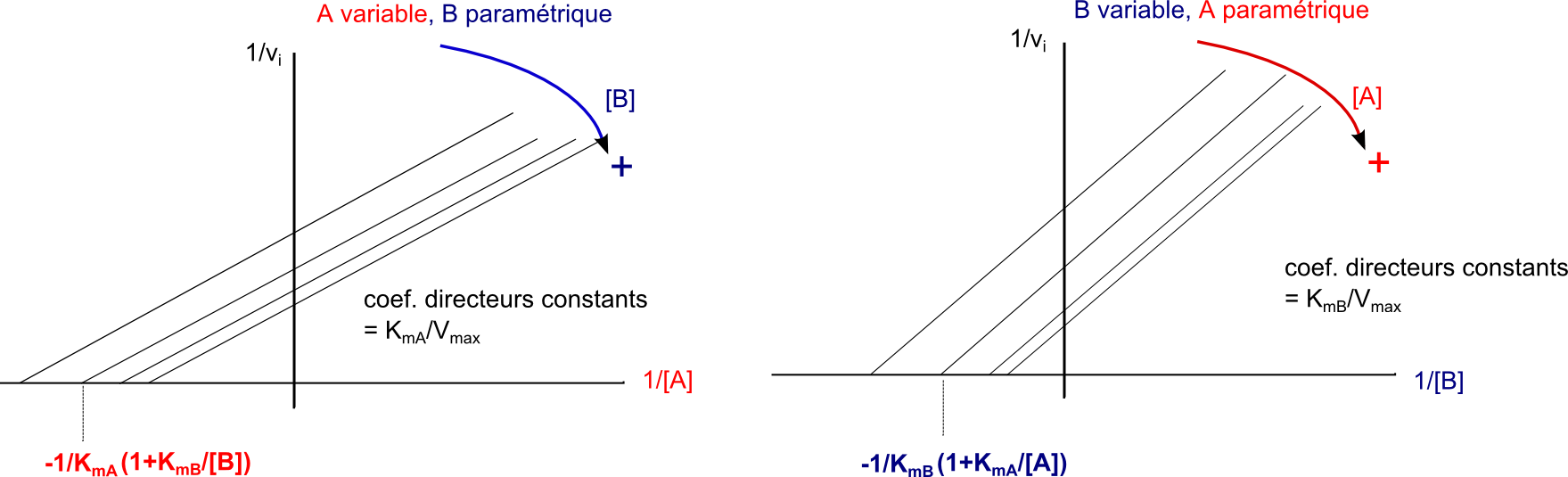
L'effet "parallélisme" est du au fait que le coefficient directeur en représentation linéarisée Lineweaver et Burk est Km/Vmax et on a vu plus haut que les rapports KmAapp/Vmaxapp sont constants à la valeur KmA/Vmax. De même pour les rapports KmBapp/Vmaxapp qui sont constants à la valeur KmB/Vmax
L'effet "parallélisme" en représentation Lineweaver et Burk (double inverse) signe le mécanisme pingpong de façon discriminante.
Le cas est détaillé sur ce même site à http://www.perrin33.com/enzym/asat_1.php