0. Densité de probabilité et fonction de répartition
Soit une variable aléatoire X (pour nous ce sera l'ensemble des résultats possibles
lors de la mesure d'une grandeur D sur un objet O donné).
On appelle fonction de répartition de X la fonction F donnant pour toute valeur x
choisie la probabilité que la variable aléatoire X soit inférieure ou égale à x.
Ce qui peut s'écrire :
F(x) = p(X<x) (où p signifie probabilité)
On peut alors définir la notion de densité de probabilité pour une varaible aléatoire.
Soit f la fonction densité de probabilité : f est la dérivée de F.
Ce qui peut s'écrire :
f(x) = dF(x)/dx
la fonction densité de
probabilité s'utilise et se "visualise" ainsi (et c'est fondamental
de bien le comprendre) : |
|
|---|---|
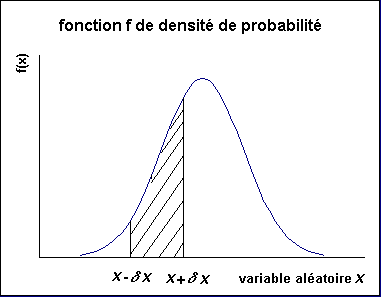
Soit p(x,δx) la probabilité que la variable aléatoire soit située entre
x - δx et x + δx ; on a : |
 |
|
La surface de la zone en hachurée sur le schéma représente la probabilité
que la variable x soit comprise entre x + δx et x - δx. |
|
Quatre fonctions de densité de probabilité et leur fonction de répartition correspondante sont très utilisées en métrologie pour les déterminations d'incertitudes : les fonctions de densité de probabilité qui correspondent aux lois dites normales, rectangulaires (ou uniformes) triangulaires isocèles et dérivée d'arc sinus.
Ces lois vous sont présentées dans les 4 paragraphes qui suivent et qui sont accessibles par le menu à gauche