1. Loi normale
La loi normale est une fonction de densité de probabilité d'équation générale : |
|
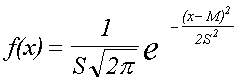 |
|
|
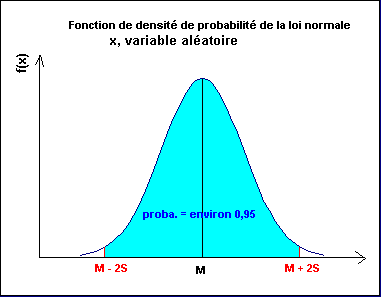
M est la moyenne, S est l'écart-type. La probabilité de x compris entre M-S et M+S est de 0,683 La probabilité de x compris entre M-1,96*S et M+1,96*S est de 0,95 La probabilité de x compris entre M-2*S et M+2*S est de 0,955 La probabilité de x compris entre M-3*S et M+3*S est de 0,997 |
Par définition, on appelle loi normale réduite, la loi normale de moyenne 0
et d'écart-type 1. Les tables statistiques de la loi normale sont
par convention celles de la loi normale réduite et sont souvent dites tables de z. Elles
fournissent des valeurs caractéristiques de probabilités associées aux lois normales.
La loi normale est appropriée pour énormément de distributions naturelles en métrologie. En effet,
beaucoup de distributions sont compatibles avec les conditions dites conditions de Borel ;
conditions que l'on peut exprimer conme suit :
Si les variations intervenant lors de chaque mesure sont la résultante
de facteurs de variations nombreux, indépendants les uns des autres, d'importances faibles
mais équivalentes alors la fonction de densité de probabilité des résultats des mesures
est une loi normale
(la validité mathématique de cet énoncé est fondée sur une loi mathématique appelée
"théorème central limite").
Et comme sur cette bonne vieille terre il y a toujours tout plein de petits facteurs de variations... et ben ça marche ... Et d'ailleurs quand on s'amuse à mesurer un objet quelconque des dizaines de fois consécutives dans les mêmes conditions d'aléa et qu'on trace la fonction de répartition des résultats, on trouve des dispersions de valeurs qui sont presque toujours en accord avec l'hypothèse de normalité ! (ça suit bien la loi normale).