• 0. déf. fonction de répartition

• 1. loi normale

• 2. loi rectangulaire

• 3. loi triangulaire isocèle

• 4. loi dérivée arc sinus

• 5. loi triangulaire asymetrique

2. Loi rectangulaire

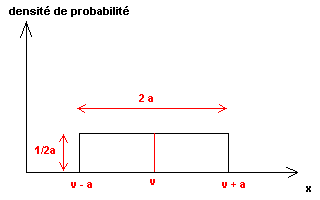
La loi rectangulaire répond à une fonction de densité de probabilité f d'équation générale : Soit v et a les deux paramètres caractérisant la fonction f. Pour x dans [v-a ; v+a]                     f(x) = 1/2a et pour (x < (v-a)) ou (x > (v+a))      f(x) = 0
	Soit S=u(x) l'écart-type, S = u(x) = a/√3. La probabilité de x compris entre v-a et v+a est de 1 (c'est à dire aussi x compris entre v±S*√3). La probabilité de x inférieur à v-a (c'est à dire aussi v-S*√3) est nulle. La probabilité de x supérieur à v+a (c'est à dire aussi v+S*√3) est nulle.

La loi rectangulaire est considérée comme appropriée pour certaines incertitudes-types. Par exemple pour les balances analytiques à lecture numérique, les certificats d'étalonnage indiquent la linéarité (qui correspond à la différence maximale entre l'affichage qu'aurait du entrainer la masse sur le plateau compte-tenu de la sensibilité et l'affichage réalisé). La linéarité est en général donnée sous la forme ± a mg. On utilise la loi rectangulaire comme appropriée pour décrire la linéarité. Ainsi la contribution de la linéarité d'une balance pour un calcul d'incertitude sera un écart-type (incertitude-type) de a/√3.