• 0. déf. fonction de répartition

• 1. loi normale

• 2. loi rectangulaire

• 3. loi triangulaire isocèle

• 4. loi dérivée arc sinus

• 5. loi triangulaire asymetrique

2. Loi triangulaire isocèle

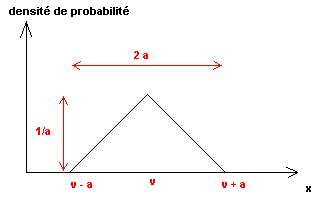
La loi triangulaire isocèle répond à une fonction de densité de probabilité f d'équation générale : Soit v et a les deux paramètres caractérisant la fonction f. Pour x dans [v - a ; v]                        f(x) = 1/a2 * x + (a - v)/a2 Pour x dans [v ; v + a]                       f(x) = -1/a2 * x + (a + v)/a2 et pour (x < (v-a)) ou (x > (v+a))      f(x) = 0
	Soit S=u(x) l'écart-type, S = u(x) = a/√6. La probabilité de x compris entre v-a et v+a est de 1 (c'est à dire aussi x compris entre v±S*√6). La probabilité de x inférieur à v-a (c'est à dire aussi v-S*√6) est nulle. La probabilité de x supérieur à v+a (c'est à dire aussi v+S*√6) est nulle.

La loi triangulaire isocèle est considérée comme appropriée pour certaines incertitudes-types. Par exemple pour de nombreuses verreries volumétriques, les certificats d'étalonnage indiquent un volume V ± a mL. On utilise généralement la loi triangulaire comme appropriée pour décrire l'incertitude sur l'étalonnage de la verrerie (on ne parle bien ici que de l'étalonnage !! pas des effets de la température et de la répétabilité des volumes distribués!). Ainsi la contribution de l'étalonnage d'une verrerie pour un calcul d'incertitude sera un écart-type (incertitude-type) de a/√6. Soit par exemple une fiole jaugée de 100 mL dont le fabricant indique ±0,1 mL à 20°C. L'incertitude-type sur l'étalonnage sera estimé à 0,1/√6. L'incertitude-type global sur le volume de la fiole devra inclure les effets de la "non maitrise" de la température et de la répétabilité ... ce qui n'est pas le propos de cette page.