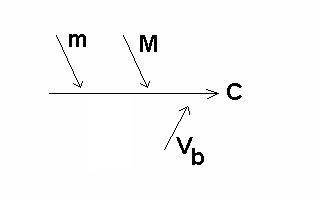
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque m, M et Vb sont des variables indépendantes.
Retour accueil | Droit de copies | Sommaire de ce dossier | Page Précédente | Page Suivante
Comment évaluer les incertitudes en analyses (bio)chimiques. Une introduction à l'aide d'un exemple simple : l'étalonnage d'une solution d'acide chlorhydrique de concentration voisine de 0,1 mol/L par pesée(s) de carbonate de sodium pur et anhydre.
1. Principe de l'étalonnage, description précise de l'étalonnage et relation fondamentale de l'étalonnage
On utilise de carbonate de sodium (diB) pur et anhydre comme étalon.
Une pesée exacte (m) de diB aux alentours de 0,17 g est mise en solution dans environ 50 mL d'eau
désionisée. On titre par la solution de HCl à étalonner afin de déterminer le volume (Vb) nécessaire pour
l'équivalence acidobasique. A l'équivalence on a la relation
2 * ndiB = nHCl .
En pratique, on réalise une pesée conventionelle de carbonate de sodium de pureté
donnée à l'aide d'une balance analytique au 1/10 de mg.
Pour déterminer Vb, le laboratoire met en oeuvre une burette automatique informatisée couplée à la mesure du pH et réalisant
le suivi en continu de la fonction pH = f(volume HCl versé). Le volume Vb
est alors déterminé par l'analyse informatique de la courbe de titration (détermination
du point d'équivalence par la méthode des dérivées premières et dérivées secondes).
Soit m la masse exacte de diB supposé parfaitement pur. Soit M la masse molaire de diB.
Soit C la
concentration de la solution de HCl.
La relation de l'étalonnage
est la suivante :
C = 2 * (m / M) * (1/Vb)
avec, par exemple, C en mol/L ; m en g ; M en g/mol ; Vb en L.
m, M et Vb sont des variables indépendantes.
Pour étalonner des solutions HCl aux environs de 0,1 mol/L avec une chutte de burette vers 18 mL, il faut réaliser des pesées exactes de diB vers (0,1 * 18 10-3 * 105,99) / 2 # 0,0954 g puisque la masse molaire de diB est de 105,99 g/mol environ. C'est ce qu'on choisit de faire.
2. Identification et analyse des sources d'imperfection dans le processus de mesure
C'est la relation d'étalonnage qui va nous donner le départ pour le recensement
des sources d'imperfection
(qui peuvent jouer à la fois au niveau d'erreurs systématiques (biais à corriger)
et au niveau de l'incertitude). A savoir :
m, M et Vb

|
Et ainsi on va commencer le travail en examinant chaque facteur d'influence de près en alliant
imagination et une bonne connaissance du processus de mesure ...
Il va falloir associer une incertitude-type et éventuellement un facteur de correction
à chaque facteur d'influence, puis combiner
correctement ces incertitudes-types pour calculer l'incertitude-type globale. La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque m, M et Vb sont des variables indépendantes. |
Déterminer l'incertitude-type sur la masse molaire (M) ne pose pas trop de problèmes. C'est par là qu'on va commencer. Il suffit d'utiliser la table des masses atomiques relatives avec les incertitudes absolues associées. Cette table est disponible auprès de l'IUPAC (International Union of Physical and Applied Chemistry). Ainsi on trouve :
Elément |
C |
Na |
O |
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page de rappel sur les fonctions de densité de probabilité avec un paragraphe concernant les distributions rectangulaires. Consultez éventuellement puis refermez. |
Masse atomique |
12,0107 |
22,989770 |
15,9994 |
|
Incertitude fondamentale donnée par l'IUPAC |
±0,0008 |
±0,000002 |
±0,0003 |
|
Soit en incertitude-type (écart-type) en supposant une distribution rectangulaire |
0,0008/√3 = 0,00046 |
0,000002/√3 = 0,0000012 |
0,0003/√3 = 0,00017 |
La formule de diB est Na2CO3 , on peut ainsi calculer la
masse molaire de diB et appliquer les propriétés de propagation des écart-types. On obtient :
masse molaire de diB (M) ; M = 2 * 22,989770 + 12,0107 + 3 * 15,9994 = 105,98844 g/mol.
Et en désignant par u(M) l'incertitude-type sur M.
u2(M) = 22 * 0,00000122 + 0,000462
+ 32 * 0,000172
= 0,000000472
___
__________
qui donne u(M) = √u2(M) = √0,000000472 = 0,00069 g/mol (expression d'une incertitude-type sur M sous forme conventionnelle d'un écart-type)
Le lien ici présent active une nouvelle ouverture de votre navigateur sur des pages de rappel sur les lois de propagation des écart-types. Consultez éventuellement puis refermez.
On va maintenant se préoccuper des imperfections sur la masse (m)
de carbonate de sodium (diB).
Et c'est là que les affaires vont commencer à se compliquer un peu ...
La pesée nous renvoie à
plusieurs sous problèmes : la répétabilité de la balance, l'incertitude sur l'étalonnage
de la balance, la question des pesées dans l'air qui ne fournissent que
des masses conventionelles et la pureté du carbonate de sodium (diB). Contentons nous pour l'instant de cette approche.
Et regardons maintenant le paramètre volume (Vb).
Là aussi, les affaires paraissent peu simples ... et on peut envisager plusieurs
problèmes :
- La question de l'incertitude d'étalonnage sur la burette ;
- La question de la répétabilité de la burette ;
- La question de la température et des variations de température dans le laboratoire.
On est alors en droit
d'envisager des problèmes de variations des volumes des solutions aqueuses voir
des volumes de
la verrerie ;
- La question d'un biais systématique sur la détermination
du point d'équivalence ainsi que la question de la répétabilité sur la détermination de Vb (liée au matériel et à la technique
de mise en évidence de l'équivalence acido-basique).
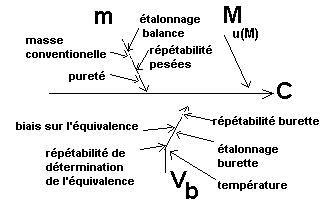
Pour ne rien oublier, inscrivons
toutes ces nouvelles problématiques
dans le "diagramme initial des causes et des effets". Qui devient :
|
Et ainsi on va continuer le travail en étudiant chaque "nouvelle" source
d'imperfection de près ...
Il va falloir associer une incertitude-type et éventuellement une correction
à chaque source, puis combiner
correctement ces incertitudes-types pour calculer l'incertitude-type globale.
La combinaison terminale ne sera pas complexe dans le cadre de l'exemple proposé puisque m, M et Vb sont des variables indépendantes. |
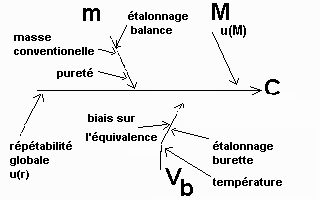
On s'intéresse alors à la question de la répétabilité. Et il apparaît qu'on peut très bien conduire une étude expérimentale statistique de répétabilité globale du dosage qui englobera en fait tous les termes de répétabilité qu'ils soient liés à la pesée, à la mesure de volume Vb où à la détermination du point d'équivalence.
On est ainsi conduit à un nouveau diagramme des "causes et des effets" associé à "une nouvelle formule" de calcul de détermination de la solution HCl à étalonner :
|
C = 2 * (m /M) * (1/Vb) * r |
Et ainsi on va continuer le travail en quantifiant le facteur répétabilité globale. Cette étude est à conduire par une analyse statistique de résultats expérimentaux en conditions de répétabilité ... Soient les valeurs suivantes obtenues après une étude statistique de répétabilité : pour le protocole à la burette automatique, suivi de pH et analyse de fonction, la répétabilité est de 0,1% en écart-type, u(r) = 0,001 et pour le protocole avec indicateur coloré de pH et burette de 25 mL, la répétabilité est de 0,25% en écart-type, u(r) = 0,0025.
On décide de s'intéresser maintenant au biais éventuel de la méthode sur la détermination du volume Vb. A priori, pour un (bio)chimiste, il n'y a aucune raison de penser à un quelconque biais pour le protocole informatisé avec analyse de la fonction pH=f(volume HCl versé). On suppose donc un biais et une incertitude-type de biais négligeable pour le protocole automatisé. Pour un protocole manuel avec indicateur coloré de pH permettant de visualiser l'équivalence , il serait légitime de se demander si il n'y a pas un biais sur le volume équivalent (pourquoi l'indicateur aurait-il un virage pile centré sur l'équivalence ?).
On choisit maintenant de considérer l'effet étalonnage de la burette. Le mode opératoire met en oeuvre une burette automatique. On suppose qu'on a employé une burette de 20 mL annoncée à ±0,03 mL par le fabricant. La loi de densité de probabilité recommandée est la loi triangulaire isocèle, on estime donc l'incertitude-type liée à la calibration de la burette à 0,03/√6=0,012 mL.
u(cal.bur.)=0,012 mL.
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page de rappel sur les fonctions de densité de probabilité avec un paragraphe concernant les distributions triangulaires isocèles. Consultez éventuellement puis refermez.
On choisit maintenant de considérer le fait que la température du laboratoire
n'est pas constante fixée à 20°C. Et 2 effets se présentent à l'esprit :
- La verrerie est étalonnée à 20°C, et le verre, comme tous les matériaux se dilate ou se contracte selon la température (le coefficient de dilation volumique des verres se situe entre
1 et 30 10-6°C-1).
- On va supposer que la solution à étalonner est destinée à une utilisation dans
le laboratoire, équilibrée à la température du laboratoire : elle peut donc se dilater
où se contracter selon les variations de température dans le laboratoire,
ce qui modifie sa concentration volumique et donc le volume pour obtenir l'équivalence.
Face à ce double constat, on est tout d'abord en droit de se demander si ce facteur d'influence "température pas vraiment contrôlée" n'est pas en fait inclu dans l'étude de répétabilité. L'idée est ici de considérer que l'étude de répétabilité à été conduite dans un laps de temps pour lequel on a vérifié que la température du laboratoire était demeurée peu variable (par exemple moins de 0,3 °C) devant les variations possibles répertoriées (par exemple 18°C à 22°C avec climatisation). Le facteur d'influence "température pas vraiment contrôlée" est ainsi exclu de l'aléa de répétabilité. Et ainsi nous allons aborder les 2 effets cités ci dessus en supposant un laboratoire climatisé à 20°C ±2°C. Classiquement les régulations en température de locaux donnent des variations sensiblement sinusoïdales entre les 2 extremums. Dans ce cas là, la fonction de densité de probabilité correspond à la une allure de type dérivée d'arc sinus, et on aura un écart-type de 2/√2 = 1,414 °C = u(δT).
On s'occupe de la dilatation du verre.La verrerie de laboratoire est étalonnée à 20°C (la température moyenne du laboratoire
avec un incertitude-type de 1,414 °C).
Classiquement, pour le verre borosilicaté, on considère que le volume de contenu possible
de la verrerie va varier avec la température d'environ 1.10-5 * V * δT
avec
V le volume "cible" et δT l'écart de la température à la référence 20°C.
On peut donc écrire que pour un volume V voisin de 18 mL délivré par la burette :
V # V20 + 1.10-5 * 18 * δT
avec V20
le volume délivré pour une température de 20°C et
δT l'écart de la température à 20°C.
Soit V # V20 + 18.10-5 δT
avec V20 et δT
deux variables indépendantes.
D'où en appliquant les lois simples de propagation des variances :
u2(V) = u2(V20) +
(18.10-5)2 * u2(δT)
Or u2(V20) n'est autre que l'incertitude-type liée à l'étalonnage de
la burette et nous connaissons sa valeur (voir ci-dessus), u(cal.bur.) = 0,012 mL. Et nous
connaissons u(δT) = 1,414 °C. Donc on a :
u2(V) = 0,0122 + ((18.10-5)2 * 1,4142)
(le terme d'effet de température est
négligeable en fait devant le terme d'étalonnage)
qui donne u2(V)= 0,00144 mL qui donne u(V) = 0,0012 mL.
Conclusion, l'incertitude-type sur le volume délivré par la burette à l'équivalence
acido-basique se résume à la seule incertitude-type sur l'étalonnage de la burette avec un
effet du facteur température tout à fait négligeable. u(V)=0,012 mL.
On choisit maintenant de considérer l'effet température sur la dilatation ou la contraction
du volume de la solution d'HCl à étalonner. Le coefficient volumique de dilatation de l'eau
est de 2,1 10-4 °C-1. Le volume de chutte de burette Vb
attendu est de 18 mL (c'est ce volume qui contient
une quantité de HCl à l'équivalence avec diB, mais ce volume aurait pu être légèrement différent et ce
selon la valeur exacte de la température
qui n'est pas contrôlée). On obtient ainsi une incertitude-type sur le volume Vb
liée au non contrôle de la température de :
u(temp_liquid) # 18 * 2,1 10-4 * 1.414 = 0,0053 mL. u(Vbeffet temp.) = 0,006 mL.
Réalisons le bilan de nos affaires de volume (étalonnage de la burette et effet température).
Puisqu'on n'examine une méthode qui ne présente pas
de biais sur
la détermination du volume équivalent,
on peut poser la relation suivante concernant le volume Vb d'équivalence acido-basique :
Vb # V + 18 * 2,1 10-4 δT
avec V et δT
deux variables indépendantes.
où V représente
le volume délivré par la burette lors de la manipulation
avec une incertitude-type u(V) et 18 * 2,1 10-4 δT le fait que le volume qu'on
trouve aurait pu être autre puisque la température du laboratoire n'est pas contrôlée.
En appliquant une méthode de calcul à l'identique de celle vue pour l'effet "dilation du verre", on obtient la relation :
_________________________
______________
u(Vb) = √ u(cal.bur.)2 + u(Vbeffet temp.)2
= √ 0,0122 + 0,0062
= 0,013 mL.
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page de rappel sur les lois de propagation des écart-types. Consultez éventuellement puis refermez.
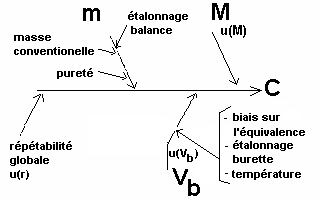
Ce calcul conduit à faire évoluer le "diagramme des causes et des effets" qui devient :
|
C = 2 * (m /M) * (1/Vb) * r |
Il nous faut maintenant nous préoccuper des causes d'incertitude qui affectent la masse (m) de carbonate de sodium (diB).
Traitons de l'incertitude-type liée à l'étalonnage de la balance pour la pesée de diB
(u(m_étalonnage)).
Deux paramètres d'étalonnage de la balance sont à considérer : la sensibilité et la linéarité.
Et ce pour une pesée en double pesée (tarage et pesée finale). Comme on travaille
avec une balance analytique sur une pesée d'une masse très faible (vers 0,0954 g) devant l'étendue des mesurages possibles et en
double pesée, l'incertitude-type liée au facteur sensibilité sera négligeable devant l'incertitude-type
liée au facteur de linéarité qui est donc le seul à considérer.
Soit la valeur de linéarité ±0,15 mg
fournie par le certificat d'étalonnage de la balance avec la recommandation d'utilisation
d'une loi de densité de probabilité rectangulaire. Exprimée en incertitude-type, on a :
u(balance_linéarité) = 0,15/√3 = 0,09 mg.
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page de rappel sur les fonctions de densité de probabilité avec un paragraphe concernant les distributions rectangulaires. Consultez éventuellement puis refermez.
Soit la considération que la pesée passe par
2 étapes : la pesée du récipient de pesée (tarage, mi) puis la pesée du récipient avec le contenu diB (valeur mf).
Soit la considération que ces 2 étapes sont indépendantes et entachés de l'incertitude-type de linéarité et que la masse
pesée est la différence entre ces 2 masses i et f. On peut écrire :
______________________________________
______________
u(m_étalonnage) = √ u(balance_linéarité)2 + u(balance_linéarité)2
= √ 0,092 + 0,092
= 0,13 mg.
Le lien ici présent active une nouvelle ouverture de votre navigateur sur une page de rappel sur les lois de propagation des écart-types. Consultez éventuellement puis refermez.
Considérons maintenant le fait que la pesée dans l'air ne nous fournit
qu'une masse conventionnelle.
La formule de correction de ce biais systématique (qui donne donc la vraie masse) est
très simple mais elle implique de
connaître la masse volumique du carbonate de sodium. Si la masse volumique du
carbonate de sodium était faible devant
la masse volumique standardisée des étalons à 8000 kg/m3, la correction ne
serait pas si négligeable que ça.
Considérons les caractéristiques du carbonate de sodium (diB) utilisé. On va supposer
que l'étalonnage met en oeuvre un étalon primaire carbonate de sodium comme décrit par
la norme ISO 6353/2 Additif 2 de novembre 1987. On y apprend que le titre (en % m/m) du produit y est
déterminé par titrimétrie potentiométrique à l'aide d'une solution d'HCl préalablement étalonnée par titrimétrie potentiométrique
avec de l'argent électrolytique. Le titre du carbonate de sodium est déterminé sur une pesée conventionelle (dans l'air)
et selon un protocole qui détermine une équivalence acido-basique. Une conclusion s'impose :
le titre ainsi déterminé est un titre qui concerne des pesées de masses conventionelles
du produit étiqueté carbonate de sodium et qui détermine des masses vraies de l'espèce moléculaire
carbonate de calcium.
On vient donc ainsi de regrouper la question de la pesée conventionelle et de la pureté.
Et on peut réécrire le diagramme des "causes et effets" ainsi :
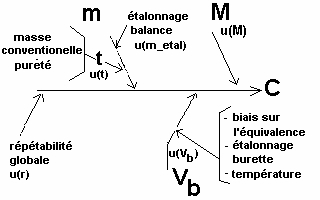
|
C = 2 * (mc * t /M) * (1/Vb) * r |
soit une spécification du carbonate de sodium indiquant 99,97 % avec un écart-type de 0,04 %. Soit t la variable associé à ce titre, on aura t=0,9997 et u(t)=0,0004.
Et voilà, on vient de terminer l'étape d'analyse et d'identification des sources d'incertitude. Si vous regardez à nouveau attentivement le diagramme des causes et des effets" présentés juste au dessus, vous verrez que toutes les incertitudes-types sont désormais estiméés. Et on a une relation simple avec des variables indépendantes en produits et quotients ! On va pouvoir se lancer dans le calcul final d'incertitude-type.
Activez ce lien pour poursuivre ...
Page mise à jour 20-12-2004 -- JF Perrin -- | Retour accueil | Droits de copies | Sommaire de ce dossier | Page Précédente | Page Suivante
Date de consultation : 26-02-2026