Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2004/2013
[A propos de l'auteur]
[Droits de copie]
Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2004/2013
[A propos de l'auteur]
[Droits de copie]
Sommaire de ce paragraphe 1 et liens internes vers les sous-paragraphes cités. |
||
1.1 Vitesse de croissance et vitesse spécifique
de croissance |
||
La vitesse de croissance à l’instant t est :
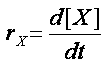(en utilisant la notation mathématique différentielle)
rX s’exprime en « concentration de biomasse . temps-1 ». (Par exemple en g.L-1.h-1.)
La vitesse spécifique de croissance à l’instant t est :
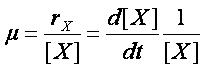
µ s’exprime en temps-1. (Par exemple en h-1 ou en min-1.)
Vous pouvez ouvrir une nouvelle fenêtre qui propose " une méthode pratique pour évaluer µ aux différents instants du suivi d'une croissance microbienne".
Pendant la phase exponentielle de croissance la vitesse spécifique de croissance (µ) est maximale et constante, on l’appelle vitesse spécifique maximale de croissance ou taux exponentiel de croissance. On la désigne généralement par µmax ou µexpo .
En phase exponentielle , 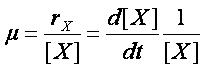est
constant et est maximum = µmax
qu’on peut intégrer
en :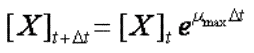 
(équation
a)
qui donne : Ln([X]t+Δt) = Ln([X]t) + µmaxΔt (équation b)
Il faut bien avoir en tête ques les 3 formules ci-dessus accompagnées de leurs conditions sont équivalentes et signifient donc exactement la même chose.
L'équation (b) est très intéressante car elle montre qu'en phase exponentielle de croissance, l'allure de la fonction ln([X])=f(t) est celle
d'une droite de coefficient directeur µmax !! Ainsi, les représentations ln([X])=f(t) présentent un double intérêt :
- intérêt visuel : l'oeil humain juge mal l'allure exponentielle mal juge bien l'allure droite ;
- intérêt pour calculer µmax lorsqu'une phase exponentielle est mise en évidence : coefficient directeur de la droite de régression sur
les points ln([X])=f(t) si il y a alignement sur une période donnée.
Vous pouvez ouvrir une nouvelle fenêtre qui illustre l'intérêt graphique des fonctions Ln(X)=f(t) et la détermination de µmax .
Remarques. On rencontre une phase exponentielle de croissance dans la plupart des cultures en milieu non renouvelé si les concentrations des différents composants sont suffisamment élevées. Dans un procédé de type chémostat (bioréacteur alimenté et prélevé en continu à même débit et en équilibre dynamique stationnaire) la vitesse spécifique de croissance est constante et est égale au "taux de dilution" si le réacteur n'est pas lavé par un débit trop élevé (taux de dilution = débit d'alimentation divisé par volume du fermenteur = débit de prélèvement divisé par volume du fermenteur). La biomasse dans le bioréacteur demeure constante car à l'équilibre dynamique atteint la croissance est égale au prélèvement.
On peut associer à µmax un certain nombre de paramètres connexes : temps de génération, taux horaire de croissance, fréquence (taux) de division par unité de temps. Ils ont l’avantage d’être plus concrets.
• Le temps de génération G, durée pour un doublement de la biomasse pendant la phase exponentielle.
En reprenant l’équation (b) pour un doublement de biomasse, on obtient :
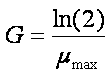
Ainsi par exemple à un temps de génération de 20 min = 1/3 d'heure correspond µmax=0,0347 min-1=2,08 h-1.
Ainsi par exemple à un temps de génération de 60 min = 1 heure correspond µmax=0,0116 min-1=0,693 h-1.
Le temps de génération est plus "parlant" pour l'esprit humain.
• Le taux de croissance horaire TCH,facteur relatif d’accroissement de la biomasse pour une durée de 1 heure, en phase exponentielle.
L’équation (a) peut s’écrire
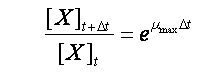donc il vient :
formule valable avec
Δt= 1 heure (soit 60 minutes)
THC est très évocateur. Ainsi pour µmax=0,0347 min-1 soit G=20 minutes = 1/3 heure on a THC = 8 (en 1 heure la biomasse est multipliée par 2*2*2=8). En 2 heures de phase exponentielle, la biomasse serait multipliée par 8*8=64 ...
• La fréquence (taux) de division en phase exponentielle, k, est finalement représentée par :
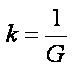et
on a la relation k = µmax Ln(2)
Remarques. On peut utiliser les puissances de 2 pour modéliser la croissance exponentielle. On fait ainsi « référence » au processus de multiplication par la division cellulaire. On obtient alors l’équation de croissance :
en effet, 
donc
avec k = µmax Ln(2) on retrouve l’équation (a)
µmax | G | THC | k |
0,0347 min-1 | 20 min | 8 = (2*2*2) | (0,05 par min) |
0,0116 min-1 | 60 min | 2 | (1/60 par min) |
0,0077 min-1 | 90 min | e^(0,0077*60) = 1,59 | (0,011 par min) |