L'essentiel à retenir

1. Vitesse initiale en enzymologie classique, état quasi-stationnaire

On réalise une cinétique enzymatique dans les conditions de l'enzymologie "classique" : tampon réactionnel donné, température constante, concentrations en substrats élevées devant la concentration en enzyme, pas de produits de réaction au temps zéro. On observe la disparition du ou d'un des substrats (S) ou l'apparition du ou d'un des produits (P) à partir de la mise en place du milieu réactionnel complet homogénéisé.

On constate alors que la vitesse de réaction, en début de réaction, apparaît comme quasi constante pendant un certain temps. Cette vitesse est appelée vitesse initiale (v_i).

Le phénomène de vitesse initiale est du à l'apparition très rapide (quasi immédiat), en début de réaction, d'un état quasi-stationnaire pour le complexe enzyme substrat (noté ES). On peut écrire que l'état quasi stationnaire en début de réaction correspond à d[ES]/dt ≈0 qui conduit à vitesse = d[P]/dt = -d[S]/dt = k₀[ES] ≈constante (où k₀ désigne le coefficient catalytique de l'enzyme). Cette vitesse quasi constante lors de l'état quasi-stationnaire de début de réaction est appelée vitesse initiale (v_i).

Avec, évidemment le pendant exact - en diminution - pour [S]=f(t).

En fait l'état quasi-stationnaire n'apparaît pas instantanément mais sa mise en place est si rapide que la phase pré-stationnaire qui le précède n'est observable qu'avec des technique particulières d'homogénéisation et d'observation.

2. Comportement Michaelien

On réalise des cinétiques enzymatiques dans les conditions de l'enzymologie "classique". On choisit un substrat observé (S) et un produit observé (P). On s'autorise les variations sur la concentration en enzyme [E]₀ et la concentration en substrat observé S au temps zéro dans le milieu réactionnel. Si les résultats cinétiques des mesures de vitesses initiales obéissent à la relation ci-dessous, alors le comportement est dit michaélien.

$$ v_i=V_{max} \frac {[S]}{K_m + [S]}~=k_0 [E]_0 \frac {[S]}{K_m + [S]} $$

Où V_max est la limite asymptotique de la vitesse initiale quand [S] tend vers l'infini. k₀ est une constante de vitesse (très dépendante de la température) appelée constante catalytique et K_m est une constante appelée constante de Michaelis pour le substrat S.

3. K_m

K_m est défini comme la concentration en substrat qui conduit à une valeur de vitesse initiale égale à la moitié de V_max (V_max étant la limite asymptotique de la vitesse initiale quand [S] tend vers l'infini). On peut aussi définir K_m comme la concentration en substrat qui permet la demi saturation de l'enzyme. K_m a la dimension d'une concentration (en substrat dans le milieu réactionnel).

K_m exprime la saturabilité de l'enzyme par S en condition de catalyse. Plus K_m est petit plus l'enzyme est facilement saturable par S (on dit aussi plus l'affinité pour S est élevée).

Pour les nombreuses enzymes pour lesquelles les actes de liaison et de séparation avec le substrat observé S sont très rapides devant les évènements catalytiques, K_m a une valeur très proche de la constante de dissociation du complexe enzyme-substrat. Mais ce n'est pas une généralité !!

4. k₀

k₀ (autre symbole officiel k_cat) est la constante catalytique de l'enzyme dans les conditions proposées. Elle correspond au nombre de rotations de l'enzyme à saturation. Sa dimension est un [temps^-1].

On a la relation V_max = k₀ [E]₀ où V_max est la limite asymptotique de la vitesse initiale quand [S] tend vers l'infini (c'est à dire la vitesse limite à saturation).

5. Modélisations classiques historiques à un substrat et un produit du comportement Michaélien

On doit à Henri, Michaelis et Menten le premier modèle de comportement Michaelien avec l'idée du complexe enzyme-substrat:

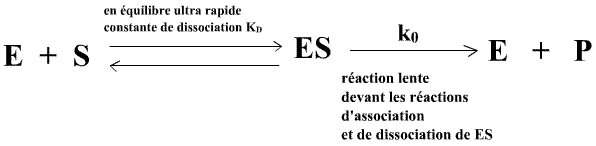
Ce modèle assimile K_m à la constante de dissociation du complexe enzyme-substrat ce qui ne convient évidemment que pour les enzymes pour lesquelles les événements d'association/dissociation de l'enzyme avec S sont très fréquents devant les évènements de catalyse.

Briggs et Haldane ont proposé une modélisation plus générale et très simple qui prend en compte l'apparition d'un état quasi-stationnaire et n'assimile pas K_m à la constante de dissociation du complexe enzyme-substrat:

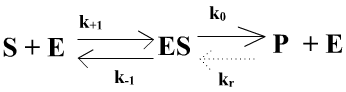
haldanemodel (3K)

Le modèle de Briggs et Haldane ne suppose pas k₀ << k₊₁ et k_-1. Mais il reste un modèle très basique et vraiment simpliste puisque à un seul substrat et un seul produit et sans comporter ni d'état de transition ni de complexe EP.

Dans le modèle de Briggs et haldane K_m = (k_-1 + k₀)/ k₊₁