Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2010-2022
[A propos de l'auteur]
[Droits de copie]
Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2010-2022
[A propos de l'auteur]
[Droits de copie]
Cette page va montrer de façon mathématique et à l'aide de modélisations informatiques la mise en place d'un état quasi-stationnaire (d[ES]dt≈0) et les conditions nécessaires dans le cadre du modèle de Briggs et Haldane. Ce qui, en soit, peut paraître de peu d'intérêt puisque le modèle de Briggs et Haldane est un modèle très simpliste ! Oui, certes. Mais je pense que ça donne beaucoup de sens à la notion d'état quasi-stationnaire. Attention cette page contient de nombreux calculs.
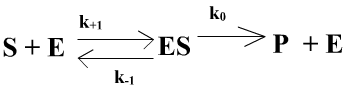
Le modèle est le suivant :
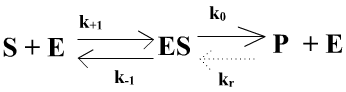
On suppose que la réaction retour de P et E vers ES est nulle (réaction irréversible) ou négligeable (début de réaction).
Au paragraphe 2 de cette page, on va montrer mathématiquement que si [S0]>>>[E0], compte-tenu des valeurs des coefficients de vitesse des enzymes, alors la fonction [ES]=f(t), en début de réaction est assimilable à :
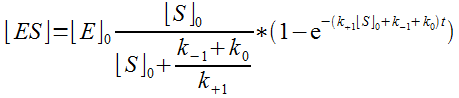
On montrera que cette fonction "flirte" très très rapidement avec son asymptote (l' état quasi-stationnaire, quasiment atteint très très rapidement) :
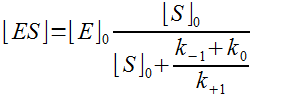
On retrouvera alors l'équation de Michaelis Menten appliqué à la "vitesse initiale" puisque la relation vitesse = k0[ES] appliquée à l'équation ci-dessus donne la formule de Michaelis et Menten.
Tout autre méthode au paragraphe 3 de cette page. On va utiliser la résolution du problème, un système de 2 équations différentielles linéaires qui n'admet pas de solution formelle à l'aide d'une modélisation informatique de son comportement à l'aide d'un petit programme écrit en langage Python. Et on devrait normalement "coller" aux résultats du paragraphe 2.
Le modèle est le suivant :
Si la réaction retour de E+P vers ES n'existe pas parce que la
transformation de S en P est irréversible où si la réaction retour de E+P vers
ES est négligeable car on se place en tout début de réaction quand [P] demeure
très faible, on peut écrire :
v = k0[ES] - kr[E][P] ≈ k0[ES]
(l'équation de base)
L'équation de base ci-dessus montre que si on connaît [ES], on connaît v. On va
donc chercher [ES]. Pour cela, on va poser une équation différentielle dont la résolution va
conduire à [ES] = f(t,[E0], [S0], k0,
k+1, k-1 ). Et on verra qu'il en découle, après une phase
préstationnaire, un état stationnaire pour [ES] et une équation v=f([S]) de forme
Michaélienne. Ce qu'on cherchait à montrer !
Le modèle de Briggs et Haldane sans réaction retour conduit de façon directe à :
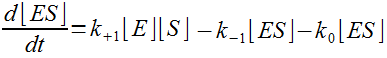
Qui donne, (en injectant le fait que [E] = [E0] - [ES]) :
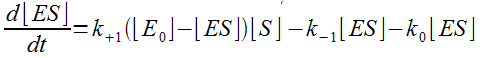
Soit en développant :
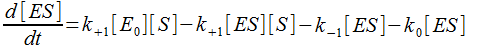
Soit en mettant [ES] en facteur :
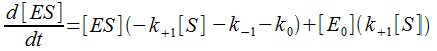
On se retrouve ainsi devant une équation différentielle qui n'est pas simple puisque [S] n'est pas obtenu de façon simple.
En effet, à chaque instant t, [S] se calcule par :
[S] = [S0] - [S engagé dans les complexes ES] - [S qui a disparu en P depuis le début de la réaction]
Soit 
(aie aie aie ! c'est l'horreur).
Mais on va faire une hypothèse qui trouvera une justification a posteriori et qui va permettre de tout simplifier. On va poser que [S] = constante = [S0] ! Ce qui n'est pas ridicule si [S0]>>>[E0] et si on se place en début de réaction quand la quantité relative de S qui a disparu reste négligeable devant [S0]. Ainsi, l'équation différentielle bien compliquée devient :
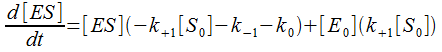(équation A)
Qui peut s'écrire :
avec
α=-k+1[S]0-k-1-k0 et
β=k+1[E]0[S]0
On va donc résoudre cette équation différentielle très simple et établir la
fonction [ES]=f(t) solution particulière correspondant aux conditions
particulières. Appelons "y" la variable [ES] et appelons "x" la variable t.
On se retrouve avec : dy/dx = αy + β c'est à dire y' = αy
+ β
Cette équation différentielle ne peut que vous avoir a été présentée en
mathématiques : équation différentielle linéaire basique ! Sa solution générale
est :
y = Ceαx - β/α avec C réel quelconque.
D'où la solution générale (en inscrivant les valeurs de α et β)
:
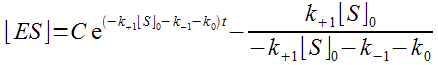
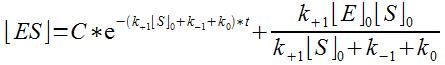
Y'a plus qu'à trouver la solution particulière correspondant aux conditions initiales.
Conditions initiales qui sont qu'à t=0 on a [ES] = 0.
On obtient ainsi (en reprenant l'équation ci-dessus avec t=0) :
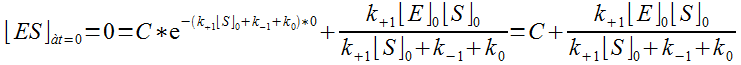
Qui donne la valeur particulère de C :
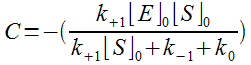
En remplaçant C par sa valeur particulière dans l'équatin solution présentée
ci-avant (équation f), on obtient :
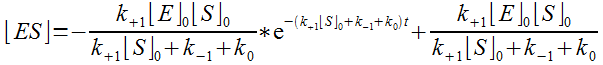
Soit, après mise en facteur :
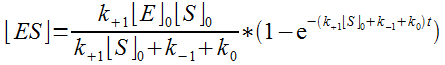
Qu'on peut écrire : (on divise numérateur et dénominateur par
k+1)
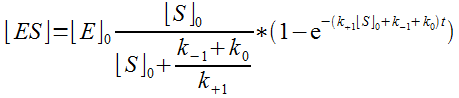(équation B)
C'est à dire : (avec Km=(k-1+k0)/k+1)
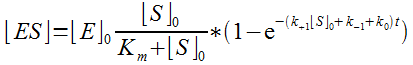
Et voilà, on y est ! C'est fini, l'équation ci-dessus donne [ES]=f(t) qu'on recherchait
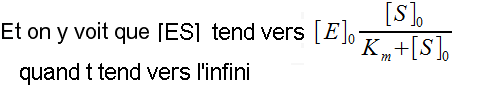
Le tableau ci-dessous propose une première application numérique.
Sont calculés à l'aide de l'équation [ES]=f(t) (équation B) établie :
- le temps nécessaire pour atteindre 99% de l'état stationnaire (en s) ; (pour ce calcul, il suffit de calculer t pour que e-(k+1[S0>]+k-1+k0)t=10-2, selon l'équation B du paragraphe précédent, soit t = 2ln(10)/((k+1[S0>]+k-1+k0) ;
- [ES] asymptotique de l'état stationnaire ;
- la vitesse initiale de réaction (=k0[ES] à la valeur asymptote) ;
- une valeur majorée de la concentration en S consommée sur la durée requise pour atteindre 99% de l'état stationnaire exprimée en mol/L et en proportion de [S0]. Ces deux dernières colonnes sont très importantes puisqu'elles justifient a posteriori la simplification posée que [S] = constante = [S0], simplification posée pour résoudre l'équation différentielle qui a conduit à établir [ES]=f(t). Il était fondamental de montrer que la consommation de S était bien négligeable, les calculs du tableau le montrent. (Pour calculer la valeur majorée de la concentration en S consommée sur la durée requise pour atteindre 99% de l'état stationnaire on a tout simplement calculé en prenant la vitesse à la valeur asymptôte de [ES] comme vitesse depuis t=0).
Données cinétiques pour les calculs |
[E0] (mol/L) |
k+1 (mol-1Ls-1) |
k-1 (s-1) |
k0 (s-1) |
Km (mol/L) |
1 10-9 |
2 107 |
2 104 |
2 103 |
1,1 10-3 |
|
Les données cinétiques ci-dessus permettent de calculer les lignes ci-dessous : | |||||
Pour [S0] de départ |
Temps pour atteindre |
[ES] état stationnaire |
vi théorique |
Consommation majorée de [S] |
Consommation majorée relative de [S] |
1,1 10-2 (S à 10Km) |
1,90 10-5 |
9,09 10-10 |
1,82 10-6 |
3,46 10-11 |
0,0000003% |
1,1 10-3 (S au Km) |
1,05 10-4 |
5 10-10 |
1 10-6 |
1,05 10-10 |
0,00001% |
1,1 10-4 (S à 0,1 Km) |
1,90 10-4 |
9,09 10-11 |
1,82 10-7 |
3,46 10-11 |
0,000032% |
Les valeurs proposées pour k+1, k-1 et k0 respectivement en mol-1Ls-1 , s-1 et s-1 sont des valeurs d'enzymes classiques. (Quoi qu'il en soit k+1 ne peut dépasser les valeurs imposées par la diffusion vers le site actif soit un plafond vers 108-109 mol-1Ls-1 pour les substrats classiques.)
Km (en mol/L) est calculé par la relation Km=(k-1+k0)/k+1.
Les valeurs pour [E0] et [S0] sont données en mol/L.
Ce sont des valeurs de milieux réactionnels enzymatiques classiques. On
remarquera que la condition [S0] >> [E0] est
toujours respectée.
On notera que la durée pour atteindre 99% de l'état quasi stationnaire est bien moindre qu'une ms avec les valeurs de coefficients de vitesse proposés !
Vous pouvez aussi télécharger le "fichier tableur - format libreOffice" suivant pour visualiser et simuler avec d'autres valeurs de coefficients (par exemple à trouver dans la littérature) : michaelis-integrationetatstationnaire-calculspratiques.ods
Le modèle est rappelé :
Qui donne le système dont le comportement est à modéliser en [ES] =f(t) et [P]=f(t) :
$$ \left\{ \begin{array}{l} \frac {d[ES]}{dt} = k_{+1}([E_0]-[ES])([S_0]-[P]-[ES]) - (k_0+k_{-1}) [ES]\\ \frac {d[P]}{dt}= k_0[ES] \\ Conditions~~initiales~~[ES]_0 ~~et~~ [P]_0=0 \end{array} \right. $$Ci-dessous voici, en image, le comportement de ce système - calculé par un programme Python -
avec les paramètres utilisés au paragraphe 2, (des paramètres standards d'enzymes), à savoir :
[E0] (mol/L) = 10-8; [S0] (mol/L) = 1,1 -3 (choisi à la valeur du Km, 1/2 saturation)) .
k+1 (mol-1Ls-1) = 2.107 ; k-1 (s-1) = 2 104 ; k0 (s-1)
=2. 103.
On y voit que l'état quasi stationnaire est bien atteint en bien moins qu'une ms !
Et pour finir, un contre-exemple. Si [E0] n'est pas tout petit devant [S0], impossible d'obtenir un état quasi-stationnaire. C'est ce que montre la modélisation informatique ci-dessous.
#import des bibliothèques de calculs numériques (numpy) et de tracés (matplot) , (en standard et pas en pylab)
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint #import de ODE intégration
k0=2 #les parametres cinetiques, valeurs standards pour enzymes. Unités temps en ms et concentrations en mmol/L
kpl1=20 #Km = (k-1+k0)/k+1 = 22/20 = 1.1 mmol/L
kmin1=20
Ezer=1e-6 #[E0] mmol/L
Szer=1.1 # [S0] mmol/L (dans le cas traité on est au Km)
def syst_eqdif(y,t): #déclaration du systeme des 2 équa dif y_1 concerne ES et y_2 le produit P (unités en mmol/L et ms !!!!)
#attention on met le y d'abord et le t ensuite !!!
y_1,y_2=y
dysurdt=[(y_1*(-k0-kmin1-(kpl1*(Szer-y_2-y_1))))+(kpl1*Ezer*(Szer-y_2-y_1)), k0*y_1]
return dysurdt
def classiq(t): #la résolution classique de ES=f(t) en supposant que Szer>>>Ezer et peu de S consommé pour atteindre un état quasi stationnaire
res_es=(((Ezer*Szer)/(((k0+kmin1)/kpl1)+Szer)))*(-1)*(np.expm1(((-kpl1*Szer)-kmin1-k0)*t))
return res_es
t = np.linspace(0,0.15, 200) #linspace définit l'étendue du tracé (ci-dessous de t=0 à la 2° valeur,) et le nbre de pts (3° valeur)
y0=[0,0] #conditions initiales pour le système des 2 équa. dif
y = odeint(syst_eqdif, y0, t) # solution (equa dif, puis on renseigne y0 puis faut avoir renseigné t avec np.linspace avant !!!)
solp = y[:,1] # les 2 tableaux des valeurs calculées par odeint solp pour y_2 (produit) et soles pour y_1 (complexe ES)
soles=y[:,0]
fig, ax1=plt.subplots() #ax1 représente la figure hôte
axy2 = ax1.twinx() #axy2 emmène l'axe 2 des y
p1, = ax1.plot(t, soles, 'b-.', label='ES (calcul odeint())') #trace ES=f(t) solution odeint
p3, = ax1.plot(t, classiq(t), 'r:', label='ES (intégration classique)') # trace ES=f(t) solution classique avec les approx classiques
p2, = axy2.plot(t, solp,'g-', label='[P] (calcul odeint()') #trace P=f(t)
ax1.legend(loc=4, borderaxespad=1.) # à placer après le plot pour faire apparaître son label quand ça ne veut pas
axy2.legend(loc=5, borderaxespad=1.)
ax1.set_xlabel('Temps ms')
ax1.set_ylabel('[ES] mmol/L', color='b')
axy2.set_ylabel('[P] mmol/L', color='g')
plt.title("Vers l'état quasi stationnaire ")
fig.tight_layout() #pour assurer les non chevauchements
plt.show() # affiche la figure a l'ecran