Les modéles de Henri Michaelis Menten et Briggs Haldane sont très simplistes puisque le complexe ES se transforme en une seule étape en produit P et enzyme libre E. Tout ça paraît évidemment trop simple. Autre critique, le modèle ne prévoit qu'un substrat et un produit, chose très rare. Voici quelques explications tentant de montrer pourquoi nos deux modèles historiques simplistes restent néanmoins très pertinents.

Avec complexe "EP", un modèle un peu plus réaliste que le modèle classique de Michaelis-Menten

Plus "réaliste" que le modèle de Michaelis-Menten et pour envisager vraiment des réactions réversibles, le modèle avec complexe EP s'écrit :

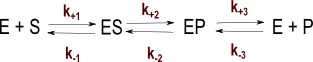modele uni uni avec EP ou pour une réaction irréversible ES EP réaction irréversible

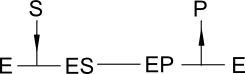
uni uni avec EP chemin

Ce modèle a le gros avantage de montrer la possibilité des inhibitions par le produit P de réaction.

Du point de vue de son traitement cinétique formel, la résolution de ce modèle à l'état quasi-stationnaire dans les conditions de vitesse initiale est :

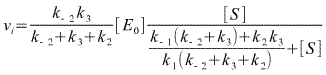
vi=f(s) avec EP

Où on voit bien ci-dessus que l'équation de vitesse a été mise sous forme michaélienne et que k0 (coefficient catalytique) et Km (coefficient de Michaelis) apparaissent comme combinaison des différents coefficients de vitesse.

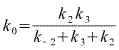k0 avec EP (On remarquera que si la réaction est irréversible ( k-2=0) et si l'acte catalytique est lent devant les associations dissociations des complexes enzymes produit (k2 petit devant k3), k0≈k2, le coefficient de vitesse de l'acte catalytique, étape limitante du processus).

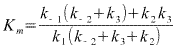km avec EP Si l'expression "cinétique" est évidemment différente de ce qu'on a vu pour les modèles de Henri et Briggs et Haldane, la signification reste la même, Km a les dimensions d'une concentration et correspond à la concentration en substrat qui conduit à vmax/2. On remarquera aussi que si la réaction est irréversible ( k-2=0) et si l'acte catalytique est lent devant les associations dissociations des complexes ES et EP (k2 petit devant k1 et k-1 et k3 et k3), k0≈k-1/k1. On retrouve évidemment le modèle de Henri !

Avec complexe de transition ES# et complexe EP

Encore plus réaliste ! Car il faut bien que la catalyse passe par un état de transition vers le produit catalysé. Le modèle devient :

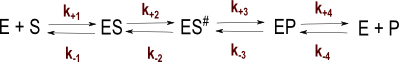
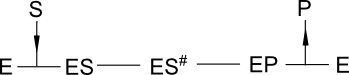
chemin reactionnel cleland

Mais ça ne change rien, l'état quasi stationnaire de vitesse initiale donnera une formalisation cinétique michaélienne ! On aura simplement des formules un peu plus complexes encore pour l'expression de k0 et Km en fonction des différents coefficients cinétiques.

Mais les réactions à un substrat et un produit sont tellement rares !

Les réactions enzymatiques qui ne mettent en jeu qu'un seul substrat et un seul produit sont rares puisqu'elles ne concernent que les isomérisations. La plupart des réactions enzymatiques impliquent 2 voire 3 substrats et libèrent 2 voire 3 produits. Toute la puissance du modèle Michaélien réside dans le fait qu'on va obtenir un comportement michaélien à 1 seul substrat et un seul produit en se plaçant comme un observateur qui ne regarde qu'un substrat comme variable (le ou les autres substrats sont en concentration paramétrique constante dans le milieu réactionnel) et un seul produit de réaction. Ceci est expliqué dans "Notion expérimentale de vitesse initiale" accessible à l'aide du menu en haut à gauche ou par le lien michaelis_1.php

Ce chapitre n'a pas pour objet de présenter le comportement michaélien des réactions à plusieurs substrats et plusieurs produits. Pour cela, voir "Comportement Michaélien et réactions à plusieurs substrats et produits"

Mais pour information, voici 3 modèles de réactions qui conduisent à des comportements michéliens quand un substrat est la variable observée, l'autre substrat étant paramétrique. A et B désignent les substrats, P et Q les produits.

Chemin réactionnel dit "ping pong" : 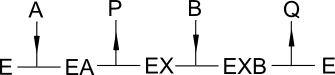bi bi ping pong

Chemin réactionnel ordonné à complexe ternaire : ordonné à complexe ternaire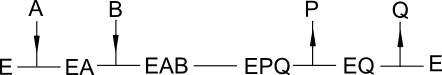

Chemin réactionnel à fixation et libération aléatoire des substrats et produits et complexe ternaire : aléatoire complexe ternaire