Retours vers :
[Accueil]
[Sommaire du dossier]
JF Perrin mise à jour 2010-2022
[A propos de l'auteur]
[Droits de copie]
La modélisation formelle dite de Briggs et Haldane (1923-1925) - qui est une généralisation du modèle historique plus simple de Henri, Michaelis et Menten - rend compte de points clés en "cinétiques enzymatiques Michaéliennes", à savoir :
- liaison réversible de l'enzyme avec le substrat en complexe ES productif de P ;
- apparition d'un état quasi stationnaire en début de réaction lorsque l'enzyme est en concentration catalytique en regard des concentrations en substrats ;
- l' allure hyberbolique "Michaélienne" des fonctions vi=f([S])
Le modèle est le suivant :
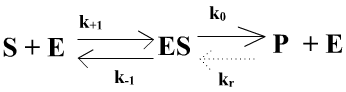
Soit v la vitesse de production de P, v = k0[ES] - kr [E][P] (rel. 1)
Si la réaction ES---> E + P est irréversible (kr = 0) ou si, dans le cas de réversibilité, on se place en début de réaction quand la réaction retour est négligeable par concentration très faible en [P] apparu, la relation 1 devient :
v = k0[ES] (rel. 2)
En pratique, avec ce modèle, compte-tenu des valeurs des coefficients k+1, k-1 et k0 des enzymes, en début de réaction, lorsque la réaction retour est négligeable , il va se former très rapidement (largement inférieur au 1/10 seconde) un état quasi stationnaire pour lequel [ES] est quasi constante (soit aussi d[ES]/dt=0). Ainsi la vitesse de réaction, en ce début de réaction en phase quasi stationnaire, sera vi = k0 [ES] ≈ constante.
Notes très importantes :
- on verra que l'état quasi stationnaire indiqué ci-dessus apparaît parce
que l'enzyme est en concentration catalytique (donc très faible devant [S]) et
parce que la réaction retour est négligeable (il y a encore très peu de P, ou
mieux : la réaction S->P est irréversible).
- La phase quasi stationnaire est en fait précédée d'une phase
préstationnaire durant laquelle [ES] augmente depuis zéro pour se stabiliser à
une quasi constance. Mais les valeurs des coefficients de vitesse des réactions
sont telles que cette phase préstationnaire a une durée si faible qu'elle n'est
pas observable avec des technologies classiques et des systèmes de mélange des
réactifs qui durent de l'oredre de la seconde. (Des techniques particulières
comme le "stop flow" permettent de suivre la phase préstaionnaire ...)
On peut essayer d'expliquer l'apparition de l'état quasi stationnaire, sans calculs mathématiques, de la façon qui suit.
Dans le texte qui suit, [E] désigne l'enzyme à l'état libre et [E0] la concentration totale en enzyme.
•1) Supposons qu'on sache homogénéiser le mélange réactionnel de façon parfaite de manière instantanée. Au "temps zéro vrai de réaction" on aurait [E] = [E0] et [ES] = 0 (en effet, au départ, tout l'enzyme est sous forme libre). Il va donc se former du ES à la vitesse vformES = k+1[E][S]. Conclusion du ES apparaît et s'accumule dans le milieu.
•2) Mais dès que du ES est présent, du ES disparaît
à la vitesse
vdispES = k-1[ES] + k0[ES] =
(k-1+k0)[ES].
•3) On voit qu'au début vformES > vdispES. Conclusion ES s'accumule dans le milieu.
•4) Mais plus [ES] s'élève, plus vdispES = (k-1+k0)[ES] devient grand
et plus vformES = k+1[E][S] devient petit puisque plus
il y a de ES moins il y a de E. En effet [E]+[ES]=[E0].
Conclusion du ES se forme mais de moins en vite et du ES disparaît mais de plus en plus vite.
•5) Arrive alors un instant pour lequel vformES = vdispES. L'état sationnaire est atteint, on a désormais d[ES]/dt = 0. Et ainsi v = k0 [ES] ≈ constante = vi.
•6) En réalité, pendant que l'état stationnaire se met en place, du substrat S est consommé ! Et donc, c'est un peu plus compliqué que ce qui est écrit au dessus ! Ce qui se met en place, c'est un état quasi stationnaire qui ne peut apparaître vraiment que si on peut considérer que la proportion de S qui disparaît (en ES et P) le temps nécessaire à son établissement est négligeable. Horreur ! Non, car c'est vrai, en pratique, avec les enzymes si la concentration initiale en S est très grande devant la concentration en enzyme totale. Ouf !
Le paragraphe intitulé "Une Equation différentielle et le modèle de Briggs et Haldane" traite tout ça de façon rigoureuse. mais y'a alors des mathématiques ...
Le schéma ci-dessous illustre les évènements.
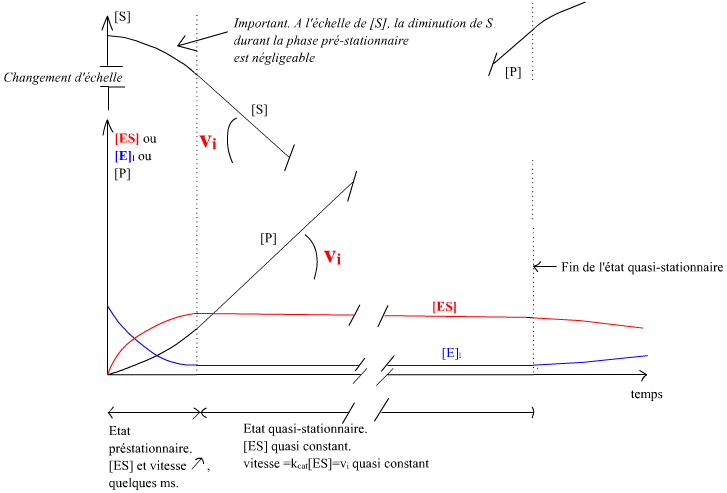
El : enzyme libre, ES complexe enzyme-substrat. Les échelles de concentrations pour l'enzyme et le substrat n'ont rien à voir ! Par construction expérimentale [S]t=0 >>> [Enzyme] . L'état préstationnaire, de durée très brève, n'est pas observable avec les techniques expérimentales classiques.
Ainsi, expérimentalement, aux échelles de temps observées et aux échelles de [S] et [P], on mesure :
 |
Technique expérimentale classique : période préstationnaire non
détectée. |
L'utilisation de l'hypothèse de l'état quasi stationnaire permet alors de "retrouver" l'équation de Michaelis-Menten.
| A l'instauration de l'état quasi stationnaire :
d([ES])/dt = 0 car vformES - vdispES= k+1[E][S] - (k-1+k0)[ES] = 0 Avec [E] = [E0] - [ES] Et on peut considérer que la concentration en [S] est encore la concentration initiale de départ. |
|
| Donc on en tire : | k+1([E0] - [ES])[S] - (k-1+k0)[ES] = 0 |
| Soit : | k+1[E0][S] - k+1[ES][S] - (k-1+k0)[ES] = 0 |
| Soit : | k+1[E0][S] - (k+1[S] + (k-1+k0))[ES] = 0 |
| Soit : | 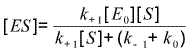 |
| Soit : | 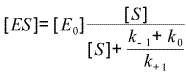 (obtenu en divisant numérateur et dénominateur par k+1) (obtenu en divisant numérateur et dénominateur par k+1) |
| Soit : | 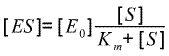 (en posant Km =
(k-1+k0)/k+1) (en posant Km =
(k-1+k0)/k+1) |
Comme vi=k0[ES], en reprenant la dernière équation du tableau, on obtient :
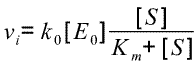 Une forme "classique"
de l'équation de Michaelis-Menten. [S] y désigne la concentration en substrat au départ dans le milieu réactionnel puisqu'on a fait
l'hypothèse [S]>>>[E0] et durée pour établir l'état quasi stationnaire très brève.
Une forme "classique"
de l'équation de Michaelis-Menten. [S] y désigne la concentration en substrat au départ dans le milieu réactionnel puisqu'on a fait
l'hypothèse [S]>>>[E0] et durée pour établir l'état quasi stationnaire très brève.
Il est très intéressant de remarquer que la dernière équation du tableau nous donne la proportion de ES - le complexe productif ! - par rapport à E0. Et que c'est cette proportion qui a une allure hyperbolique et montre un effet de saturation pour lequel [ES] tend vers [E0] quand [S] tend vers l'infini (c'est à dire quand [S] est grand devant Km). On trouvera évidemment [ES] = [E0]/2 lorsque [S]=Km : on est alors à Vmax/2.