Modèle historique de Henri, Michaelis et Menten

On doit à Henri, vers 1903, la modélisation formelle suivante :

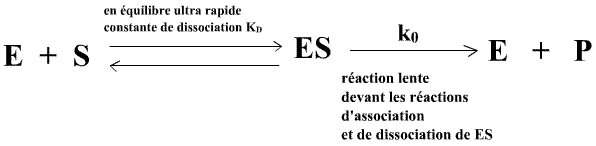
michaelis-img-henri (5K)

On doit à Michaelis et Menten, vers 1913, la "validation convaincante" expérimentale de ce modèle et sa "mise en forme" historique.

Selon ce modèle, les réactions d'association et de dissociation du complexe [ES] étant extrèmement rapides devant la réaction de ES produisant E et P : E, S et ES sont en quasi équilibre :
Soit KD la constante de dissociation de ES, on a : KD ≈ [E][S]/[ES]

C'est à dire KD ≈ ([E0]-[ES])[S]/[ES]

C'est à dire [ES]KD = ([E0]-[ES])[S] = [E0][S]-[ES][S]

C'est à dire [ES]KD + [ES][S] = [E0][S]

C'est à dire [ES](KD + [S])= [E0][S]

C'est à dire 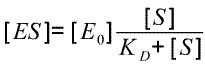michaelis-img-eq51 (2K)

Comme la concentration en S est très grande devant la concentration en enzyme, on peut considérer qu'en vitesse initiale, la concentration en S dans le milieu réationnel est assimilable à la concentration en S initiale dans le milieu réactionnel.

Comme vitesse de formation de P = v=k0[ES] (en regardant le modèle proposé). On en déduit :

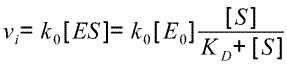
michaelis-img-eq52 (2K)

On a là la forme "Michaélienne" de l'équation de vitesse initiale. [S] y est assimilable à [S] initiale dans le milieu réactionnel. k0[E0]=Vmax et Km est assimilable à KD c'est à dire à la constante de dissociation du complexe enzyme-substrat (mais ceci n'est valable que dans le cadre du modèle de Henri).

Km dans le modèle de Henri-Michaelis-Menten et Km dans le modèle de Briggs et Haldane

On vient de le voir, dans le modèle de Henri, Km est assimilable à KD la constante de l'équilibre ES=E+S. Et ce parce que le modèle suppose que l'acte catalytique de transformation de ES en E + P est rare devant les associations "E+S donne ES" et les dissociations "ES en E et S" ! Autrement formulé : l'enzyme s'associe et se dissocie du substrat extrêmement vite et, de temps en temps seulement (même si ça nous paraît rapide à nous), arrive enfin à catalyser ES en S et P. Si ce modèle a encore du succès, c'est parce que ceci est vrai pour beaucoup d'enzymes. Et donc pour celles là (et celles là seulement!) Km est assimilable à KD.

On l'a vu, dans le modèle de Briggs et Haldane, il n'y a pas besoin de supposer que l'acte catalytique est rare devant les associations/dissociations entre E et S. Ce modèle conduit à Km = (k-1+k0)/k+1). Or KD = k-1/k+1. Donc Km et KD ne sont pas assimilables ! Si on y regarde de près, on voit que si k0 est très petit devant k-1, on a Km ≈ k-1/k+1 = KD. Le modèle de Henri est en fait un cas particulier du modèle plus général de Briggs et Haldane. Tout va bien.

Il est très important de retenir qu'assimiler Km et KD n'est possible que pour les enzymes pour lesquelles l'acte catalytique de transformation de ES en E + P est rare devant les actes d'association E+S donne ES et de dissociation de ES en E et S. Et que ceci n'est vrai que pour certaines enzymes. On ne peut donc absolument pas définir Km comme une mesure de l'affinité de l'enzyme pour le substrat puisque ce n'est vrai que pour certaines enzymes. Il faut s'en tenir à une définition générale : Km, concentration en substrat qui conduit à la demi-saturatiuon de l'enzyme, c'est à dire à vitesse initiale = moitié de la vitesse maximale.